Resumo sobre Números Primos

Neste artigo, “Resumo sobre Números Primos”, objetivando ajudar você, candidato, reunimos todos os tópicos fundamentais para fazer uma base sólida sobre o tema.

Apresentação do Assunto

Antes de tudo, é relevante destacar que o estudo desse assunto constitui um alicerce da Aritmética. Dessa forma, compreender sua definição e propriedades é essencial para resolver questões.

Esses números atuam como os “blocos de construção” de todos os números naturais. Sem eles, não conseguiríamos realizar operações fundamentais como o cálculo do Mínimo Múltiplo Comum (MMC) ou do Máximo Divisor Comum (MDC).

Sendo assim, estruturaremos este tema nos seguintes tópicos:

• Definição e Conceitos Básicos
• O Caso dos Números 0 e 1
• O Número 2: O Único Primo Par
• Números Primos x Compostos
• Reconhecimento de Números Primos
• O Crivo de Eratóstenes
• Teorema Fundamental da Aritmética
• Números Primos entre Si
• Conclusão do Artigo

Definição e Conceitos Básicos

Primeiramente, salienta-se que um número natural é considerado primo quando possui exatamente dois divisores naturais distintos: o 1 e ele mesmo. Essa regra é rígida e não admite exceções dentro do conjunto dos Naturais.

Além disso, representamos o conjunto dos números primos pela letra P. A sequência inicia-se da seguinte forma: 2, 3, 5, 7, 11, 13, 17, 19, 23, …

Apesar de a sequência acima ser infinita, as bancas frequentemente elaboram questões que exigem o reconhecimento rápido desses valores até o número 50 ou 100. Portanto, é fundamental que o candidato memorize os primeiros números primos.

O Caso dos Números 0 e 1

Inicialmente, no contato primário com o assunto, muitos candidatos cometem erros ao classificar os números 0 e 1. O 0 não é primo, pois possui infinitos divisores (qualquer número divide zero, exceto o próprio zero).

Assim como o 0, o 1 também não é primo. Isso acontece porque ele possui apenas um divisor (ele mesmo), o que viola a regra de ter “dois divisores distintos”. Portanto, o 1 não é nem primo.

O Número 2: O Único Primo Par

O 2 possui uma característica única no conjunto dos números primos. Ele é o único que é par. Todos os demais números pares são divisíveis por 2, além de 1 e deles mesmos, o que os torna compostos.

Logo, essa propriedade facilita a eliminação de alternativas em provas. Se uma questão pergunta sobre um número primo grande, você pode descartar imediatamente qualquer um terminado em 0, 2, 4, 6 ou 8 (exceto o próprio 2).

Números Primos x Compostos

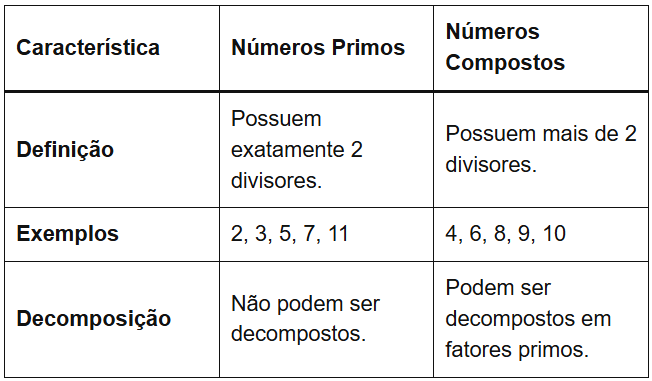
Primeiramente, diferenciamos os números naturais maiores que 1 em duas categorias principais: primos e compostos. Dessa forma, entender essa distinção é crucial para a decomposição numérica.

Os números compostos são aqueles que possuem mais de dois divisores. Ou seja, além de serem divisíveis por 1 e por eles mesmos, possuem pelo menos um terceiro divisor.

Por exemplo, o número 4 é composto pois seus divisores são {1, 2, 4}. O número 6 também é composto, com divisores {1, 2, 3, 6}. Todo número composto pode ser escrito como uma multiplicação de números primos.

Por fim, para facilitar o entendimento, apresentamos o seguinte quadro comparativo:

Reconhecimento de Números Primos

Primeiramente, identificar se um número pequeno é primo é uma tarefa simples. No entanto, para números maiores, precisamos de um método sistemático para não perder tempo na hora da prova.

Assim, o método mais eficiente é a tentativa de divisão. Devemos dividi-lo pelos números primos sucessivos (2, 3, 5, 7, 11…) até que ocorra uma das duas situações abaixo.

Primeira situação: encontramos uma divisão exata (resto zero). Nesse caso, ele não é primo, pois descobrimos um divisor além de 1 e dele mesmo.

Segunda situação: o quociente da divisão torna-se menor ou igual ao divisor, e a divisão não foi exata. Nesse caso, podemos parar as tentativas e afirmar que ele é primo.

Exemplo Prático de Verificação

Primeiro passo para verificarmos se o número 113 é primo:

• Não é par (não divisível por 2).
• Soma dos algarismos é 5 (não divisível por 3).
• Não termina em 0 ou 5 (não divisível por 5).

No segundo passo, continuamos as divisões:

• 113/7 gera um quociente igual a 16 e resto 1 (diferente de 0)
• 113/11 gera um quociente igual a 10 e resto 3 (diferente de 0)

Pare aqui! O quociente (10) tornou-se menor que o divisor (11). Como não houve divisão exata até esse ponto, concluímos com certeza que 113 é primo.

O Crivo de Eratóstenes

Para encontrar todos os números primos até um determinado valor limite, utilizamos o algoritmo conhecido como Crivo de Eratóstenes. Este método é visual e excelente para o aprendizado inicial.

O processo consiste em listar todos os números naturais até o limite desejado. Primeiro, eliminamos o número 1. Em seguida, circulamos o 2 e eliminamos todos os seus múltiplos.

Depois, circulamos o próximo número não riscado (o 3) e eliminamos seus múltiplos. Repetimos o processo sucessivamente. Os números que restarem sem ser riscados são os números primos.

Teorema Fundamental da Aritmética

Este é um dos conceitos mais importantes da matemática elementar. O teorema afirma que todo número natural maior que 1 ou é primo ou pode ser escrito como um produto de números primos de maneira única.

Isso significa que os números primos são os “átomos” da matemática. Qualquer número composto é formado pela multiplicação exclusiva de primos. Esse processo chama-se fatoração ou decomposição.

Processo de Fatoração

Para decompor um número, realizamos divisões sucessivas pelo menor divisor primo possível. O resultado da divisão é utilizado na próxima etapa, até chegarmos ao quociente 1.

Vejamos a decomposição do número 60:

1. 60/2 = 30
2. 30/2 = 15
3. 15/3 = 5
4. 5/5 = 1

Percebe-se, então, que a forma fatorada de 60 é 2x2x3x5 ou, utilizando potências, 2²x3x5. Dessa forma, o domínio dessa técnica é obrigatório para questões de MMC e MDC.

Números Primos entre Si

Um conceito que causa confusão, mas é vital, é o de primos entre si (ou coprimos). Dois números são primos entre si quando o único divisor comum entre eles é o 1.

Além disso, é mportante notar: os números em si não precisam ser primos. A propriedade refere-se à relação entre eles. O seu Máximo Divisor Comum (MDC) deve ser igual a 1.

Exemplo: Os números 8 e 9.

• Divisores de 8: {1, 2, 4, 8} (Note que 8 não é primo).
• Divisores de 9: {1, 3, 9} (Note que 9 não é primo).

O único divisor que aparece em ambas as listas é o 1. Portanto, MDC(8, 9) = 1. Logo, 8 e 9 são primos entre si, embora sejam individualmente compostos.

Conclusão do Artigo

Chegamos, então, ao fim do nosso artigo. Nele, aprendemos a definição do termo, discutimos a importância do 2 como único par e a apresentamos a diferença crucial entre ser primo absoluto e ser primo entre si. Sendo assim, de modo a facilitar a memorização dos principais números primos, construímos a seguinte tabela:

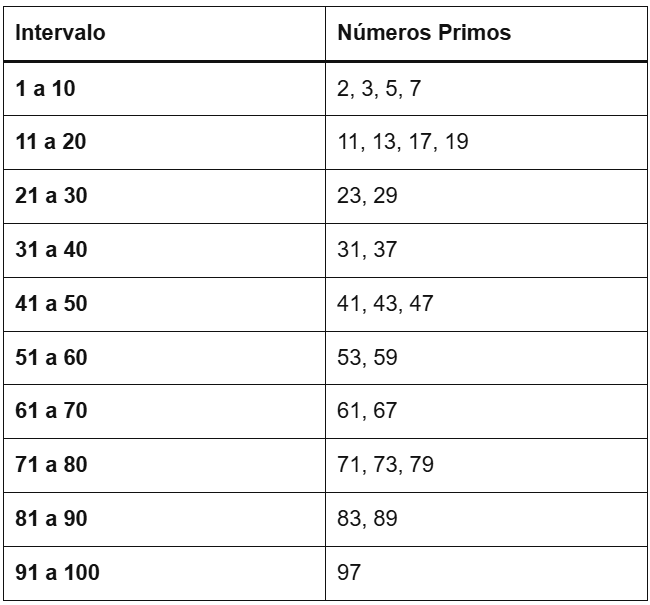
Portanto, note que o número 91 não está na lista. Apesar de confudirem frequentemente com um número primo, ele não é, pois 91 = 7×13. Assim, fique atento a essa “pegadinha” comum em provas.

Por fim, para consolidar todo conhecimento aprendido neste artigo, vá até o Sistema de Questões do Estratégia e comece já o treinamento!

ASSINE AGORA –Assinaturas

Assine agora a nossa Assinatura Anual e tenha acesso ilimitado a todos os nossos cursos.

Fique por dentro de todos os concursos:

Concursos abertos

Concursos 2026