Resumo sobre as Leis de Morgan
Fala, estrategistas! Vamos aprender sobre as Leis de Morgan hoje!
Essas leis são princípios fundamentais da lógica matemática e têm aplicações importantes na computação, engenharia elétrica e em qualquer área que envolva a lógica booleana.

Entendendo as Leis de Morgan
As Leis de Morgan descrevem como as negações se comportam quando aplicadas a proposições compostas usando os operadores lógicos E (^ – conjunção) e OU (v – disjunção).
Vamos agora analisar cada uma das leis em nosso artigo.
Primeira Lei de Morgan
A primeira lei descreve que negar duas proposições simples que estão compostas pelo operador E (p ^ q) é o mesmo que negar as duas proposições e trocar seu operador pelo OU (v).
Ou seja:
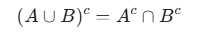
Assim, a negação de uma conjunção (e) é equivalente à disjunção (ou) das negações.
Vamos dar exemplos para ilustrar melhor.
- Imagine a seguinte afirmação: “Eu vou à praia e vou tomar sorvete.”
Se quisermos negar essa frase inteira (dizer que ela é falsa), não basta negar apenas um item. Seguindo a regra:
- Proposição P: Eu vou à praia.
- Proposição Q: Eu vou tomar sorvete.
- Negação: “Não é verdade que (eu vou à praia e tomo sorvete)”.
Resultado pela Lei de De Morgan:
“Eu não vou à praia ou eu não vou tomar sorvete.”
Dessa forma o conectivo “ou” significa que pelo menos uma das coisas não aconteceu (ou ambas).
- Considere a proposição onde x deve atender a duas condições simultâneas:
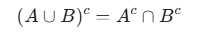
Para negar essa afirmação, aplicamos a lei invertendo o conectivo e negando as condições individuais:
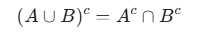
Resultado:
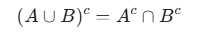
Resumindo:
Para aplicar a Primeira Lei de De Morgan, você realizará os seguintes passos:
- Negar a primeira parte.
- Trocar o sinal de “e”
- Negar a segunda parte.
Segunda Lei de Morgan
Já a segunda lei, temos que a negação de duas proposições conectadas com o OU (p v q) é o mesmo que negar as duas proposições e modificar seu operador para E (^):
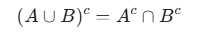
Assim, para negar que uma coisa ou outra aconteceu, você deve provar que nenhuma das duas aconteceu.Vamos aos exemplos:
- Imagine que uma regra de um concurso diz: “Para entrar, você deve ser professor ou ser estudante.”
Se você quiser afirmar que alguém não cumpre essa regra (a negação), você diria:
- Proposição P: É professor.
- Proposição Q: É estudante.
- Negação: “Não é verdade que (é professor ou é estudante)”.
Pela Segunda Lei de De Morgan:
“Ele não é professor e não é estudante.”
- Na teoria dos conjuntos, a Segunda Lei de De Morgan diz que o complementar da união de dois conjuntos é igual à interseção dos complementares desses conjuntos.
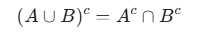
Isso significa que tudo o que está fora da “bolha” de A e B juntos é exatamente o que está fora de A e, ao mesmo tempo, fora de B.
Aplicação em Conjuntos
Os conjuntos de elementos são frequentemente representados por letras maiúsculas.
Esses elementos se relacionam de forma que podem conter uns aos outros, ou compartilhar elementos.
Conjunto U (universo. Ou seja, todos os elementos) = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
Conjunto A = {1, 2, 3, 4, 5}
Conjunto B = {4, 5, 6, 7, 8, 9, 10}
A U B (A unido a B): conjunto composto por todos os elementos de A, junto a todos os elementos de B = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
A ∩ B (Interseção de A e B): conjunto composto por todos os elementos que estão contidos em A e também em B = {4, 5}
A’ (complemento de A): tudo que não está contido em A = {6, 7, 8, 9, 10}
B’ (complemento de B): tudo que não está contido em B = {1, 2, 3}
As Leis de Morgan se aplicam a conjuntos:
- Complemento da interseção: (A ∩ B)’ = A’ U B’ – Lê-se: o complemento da interseção de A com B é igual ao complemento de A unido ao complemento de B;
- Complemento da união: (A U B)’ = A’ ∩ B’ – Lê-se: o complemento da união de A com B é igual à interseção do complemento de A com o complemento de B.
Curiosidades
Augustus de Morgan era um lógico e matemático que nasceu na Índia no ano de 1806, na cidade de Madurai.
Seus pais eram ingleses, porém seu pai estava em uma missão militar no território indiano quando Augustus nasceu.
Em 1923, Morgan começou seus estudos na Universidade de Cambridge, mas não conseguiu dar continuidade a eles. Na época, não quis se submeter a um exame religioso.
No ano de 1827, candidatou-se à cadeira de Matemática na nova Universidade de Londres, mesmo sem ter realizado publicações na área de matemática.
Em 1828, recebeu a nomeação como o primeiro docente de Matemática da Universidade. Augustus foi responsável por introduzir as Leis de Morgan, e sua obra mais notável é “Formal Logic”, onde ele apresentou uma nova abordagem para a Lógica Matemática.
Por hoje é isso, pessoal!
Abraços e até a próxima.
Bárbara Rocha
Assista as nossas aulas para aprofundar-se nos temas e obter sucesso na sua aprovação :)
ASSINE AGORA – Assinaturas
Assine agora a nossa Assinatura Anual e tenha acesso ilimitado* a todos os nossos cursos.
Fique por dentro de todos os concursos: