Saiba tudo sobre a Definição de Matemática

Entender a “Definição de Matemática” é importante para fazer uma base sólida na disciplina de Raciocínio Lógico-Matemático. Objetivando ajudar você, candidato, reunimos o essencial sobre essa temática neste artigo!

Antes de tudo, é relevante destacar que esse assunto é o primeiro passo para compreender a forma como essa matéria é definida e estruturada.

Sendo assim, organizamos este tema por meio dos seguintes tópicos:

• Estruturação e Definição de Matemática para Concursos;
• Conceito Fundamental e Etimologia;
• A Matemática como Ciência Formal;
• O Método Axiomático e a Lógica;
• As Grandes Áreas da Matemática;
• Conclusão do Artigo “Saiba tudo sobre a Definição de Matemática”.

Estruturação e Definição de Matemática para Concursos

Primariamente, a matemática é vista apenas como o estudo dos números. Contudo, essa ciência é, na verdade, muito mais abrangente e profunda.

Uma boa definição de matemática é que ela é a ciência do raciocínio lógico e abstrato, que estuda padrões, estruturas, formas e mudanças. Ela não se limita a fazer contas, mas busca descrever e entender as relações entre objetos abstratos.

Dessa forma, para o candidato, compreender essa natureza lógica é essencial. Isso acontece porque as bancas examinadoras valorizam a capacidade de aplicar definições precisas para resolver problemas complexos, exigindo mais do que simples memorização de fórmulas.

Conceito Fundamental e Etimologia

Inicialmente, é importante apresentar a natureza etimológica da palavra. Dessa forma, conforme o Dicionário Etimológico, “matemática” deriva do grego matemathike, sendo máthema equivalente à compreensão, explicação, ciência, conhecimento e aprendizado e thike igual à arte. Portanto, em sentido amplo, uma outra definição de matemática é que ela é a arte ou técnica de explicar, de conhecer, de entender os entes abstratos e suas propriedades.

Historicamente, a matemática surgiu da necessidade prática de contar, medir terras e prever eventos astronômicos. Com o tempo, ela evoluiu para um sistema puramente teórico, desvinculando-se da necessidade imediata de aplicação física.

Hoje, definimos a matemática como uma linguagem universal. Ela possui vocabulário e regras gramaticais próprias (sintaxe) que permitem comunicar ideias complexas com total precisão, eliminando as ambiguidades das línguas naturais.

A Matemática como Ciência Formal

Ainda relacionada à ideia de definição de matemática, pode-se afirmar que ela não é uma ciência natural ou empírica, diferente da Biologia ou da Física. Assim, a matemática é classificada como uma ciência formal. Isso significa que suas verdades não dependem de experimentos em laboratório para serem comprovadas.

Nas ciências naturais, uma teoria é validada pela observação da natureza. Na matemática, a validade de uma afirmação depende exclusivamente da sua consistência lógica com as regras estabelecidas previamente.

Portanto, um teorema matemático, uma vez provado, é uma verdade eterna. O Teorema de Pitágoras, demonstrado na Grécia Antiga, continua verdadeiro hoje e continuará para sempre, independentemente de mudanças no mundo físico.

Por fim, abaixo, apresentamos um quadro comparativo para fixar a diferença entre ciências formais e empíricas:

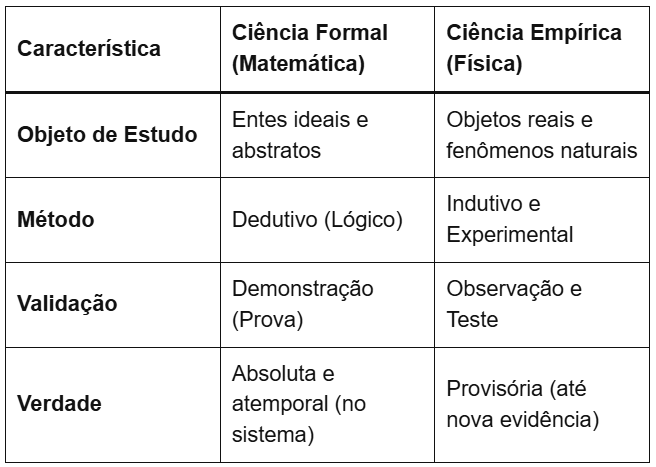
O Método Axiomático e a Lógica

Primeiramente, destaca-se que a estrutura da matemática se baseia no método axiomático. Tudo começa com axiomas (ou postulados), que são verdades iniciais aceitas sem demonstração por serem evidentes ou definidas como ponto de partida.

A partir desses axiomas, utilizamos o raciocínio lógico para deduzir novas verdades, chamadas de teoremas. Esse processo de construção garante que o edifício matemático seja sólido e livre de contradições internas.

Para o concurseiro, isso explica a importância da lógica proposicional. Entender conectivos lógicos (“e”, “ou”, “se… então”) é manipular a própria estrutura de construção do conhecimento matemático.

As Grandes Áreas da Matemática

Para fins didáticos e de estudo, costumamos definir a matemática por meio da divisão em grandes ramos, embora ela seja uma só. Essa divisão facilita a organização do conteúdo nos editais de concursos públicos.

A Aritmética é o ramo mais básico, lidando com os números e as operações fundamentais. É a base para o estudo de quantidades e serve de alicerce para praticamente todas as outras áreas.

A Álgebra introduz a abstração ao utilizar letras e símbolos para representar números desconhecidos ou conjuntos de números. Ela estuda as estruturas, as equações e as regras gerais de manipulação desses símbolos.

A Geometria foca no estudo das formas, tamanhos e propriedades do espaço. Ela pode ser plana (duas dimensões) ou espacial (três dimensões), sendo crucial para provas que envolvem visualização e medidas.

Por fim, temos a Análise (que inclui o Cálculo), que estuda a mudança e o infinito. Embora menos cobrada em concursos de nível médio, é fundamental para cargos de nível superior em áreas exatas e econômicas.

Conclusão do Artigo “Saiba tudo sobre a Definição de Matemática”

Chegamos ao fim da nossa exposição sobre a definição de matemática. Compreendemos que ela é a ciência dos padrões e do raciocínio dedutivo, fundamentada em axiomas e estruturada pela lógica.

Percebe-se, portanto, que dominar a matemática exige mais do que decorar tabuadas. Requer o desenvolvimento de um pensamento estruturado, capaz de operar com conceitos abstratos e realizar deduções precisas.

Além disso, lembre-se de que essa base teórica é o que sustentará seu aprendizado de tópicos específicos. Utilize esse conhecimento para encarar as questões de prova com um olhar analítico e rigoroso.

Por fim, para consolidar todo conhecimento aprendido neste artigo, vá até o Sistema de Questões do Estratégia e comece já o treinamento!

ASSINE AGORA –Assinaturas

Assine agora a nossa Assinatura Anual e tenha acesso ilimitado a todos os nossos cursos.

Fique por dentro de todos os concursos:

Concursos abertos

Concursos 2026