Fala, estrategistas! Vamos aprender hoje sobre a Sequência de Fibonacci? Trata-se de uma sequência de números desenhada pelo matemático Leonardo Pisa, mais conhecido como Fibonacci.
Essa sequência é crescente, é infinita, é formada apenas por números naturais. Não há negativos, frações ou irracionais.
A principal característica da sequência está em sua lógica de formação.
A regra principal para a formação da sequência é a seguinte: do terceiro termo em diante, cada novo termo é a soma dos dois termos anteriores.
O ínicio é o número 1, sendo o segundo termo também o número 1, o terceiro é o número 2, pois 1 + 1 = 2.
Por sua vez, o quarto termo será o 3, uma vez que o segundo termo é o 1, e o terceiro o 2, o quarto só pode ser o 3, pois: 1 + 2 = 3.
Sendo assim, são os primeiros 11 termos da sequência:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, …
Trata-se do exemplo clássico dos coelhos, onde a Sequência de Fibonacci descreve o crescimento de uma população desses animais.
A sequência é definida mediante a seguinte fórmula:
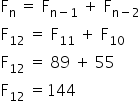
Onde:
é um termo qualquer, ou, enésimo termo. Na matemática, o “n” é por vezes usado como um índice para se referir a um elemento qualquer de uma sequência.
é o termo anterior ao que Fn, é o antecedente.
é o temo anterior à Fn-1. Ou seja, duas posições atrás de Fn.
Sendo assim, observa-se que a sequência de Fibonacci é a forma algébrica de dizer que um termo qualquer na sequência é a soma dos seus dois anteriores.
Exemplo
Calcule o 12º termo da sequência Fibonacci sabendo que os anteriores são 89 e 55.
Resolução
Sendo n = 12, décimo segundo termo é .
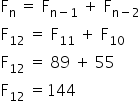
e
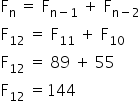
Pela fórmula:
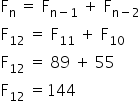
Logo, o décimo segundo termo da sequência é o 144.
Utilizando esta lógica ou com o auxílio da fórmula, obtemos os próximos termos da sequência. Aqui está uma lista com os 30 primeiros termos da Sequência Fibonacci, 10 por linha:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55,
89, 144, 233, 377, 610, 987, 1 597, 2 584, 4 181, 6 765,
10 946, 17 711, 28 657, 46 368, 75 025, 121 393, 196 418, 317 811, 514 229, 832 040
Repare que a sequência cresce em valores rapidamente. Para se ter ideia, o centésimo termo da sequência é o número 354 224 848 179 261 915 075 ou, aproximadamente .
A partir dessa sequência, pode ser construído um retângulo, chamado de Retângulo de Ouro, uma representação visual da sequência.
No desenvolvimento do retângulo de ouro, dois quadrados com lados de unidade 1 são postos lado a lado. Eles representam os dois primeiros termos da sucessão.
Como o terceiro termo é 1 + 1 = 2, um terceiro quadrado com lado medindo 2 unidades é desenhado.
Ao desenhar um arco dentro desse retângulo, obtemos, por sua vez, a Espiral de Fibonacci.
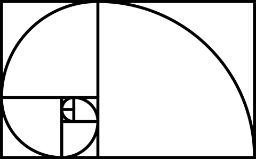
Espiral de Fibonacci
Na natureza podemos perceber a sequência de Fibonacci nas folhas das árvores, nas conchas dos caracóis, dos frutos e até mesmo nas galáxias.
A sequência de Fibonacci pode ser aplicada na matemática, nas ciências aplicadas e até mesmo no design.
Por meio do coeficiente de um número com o seu antecessor, obtém-se a constante com o valor aproximado de 1,618.
Aplicam-se também em análises financeiras e na informática, sendo utilizada por Leonardo Da Vinci, que chamou a sequência de Divina Proporção, realizando seus desenhos perfeitos.
Na Biologia a sequência descreve padrões de crescimento em plantas e animais. A arte, o design e a arquitetura se inspiram para criar desde obras de arte a construções. No campo da matemática e computação, ela contribui com aplicações na teoria dos números, estudos de sequências, algoritmos e ciência da computação.
Leonardo Fibonacci era conhecido como Leonardo Pisano ou de Pisa, um matemático italiano nascido no final do século XII que introduziu o sistema numérico hindu arábico.
Aprendeu as técnicas da matemática por meio de viagens em países da Europa, África e Oriente Médio. Contribuiu para o Renascimento das Ciências Exatas na Antiguidade Clássica e na Idade Média.
Atualmente, temos a aplicação prática da Sequência de Fibonacci até mesmo no mercado de ações. Alguns matemáticos defendem que as flutuações do mercado financeiro obedecem um padrão de crescimento e decrescimento que acompanham essa sequência.
Por hoje é isso, pessoal!
Abraços e até a próxima.
Bárbara Rocha
Assista as nossas aulas para aprofundar-se nos temas e obter sucesso na sua aprovação :)
ASSINE AGORA Assinaturas
Assine agora a nossa Assinatura Anual e tenha acesso ilimitado* a todos os nossos cursos.
Fique por dentro de todos os concursos: