Gabarito PF Raciocínio Lógico: Agente, Escrivão e Papiloscopista
Fala, pessoal!
Sou o Eduardo Mocellin, professor de Matemática e de Raciocínio Lógico do Estratégia Concursos.
A seguir, disponibilizo o gabarito extraoficial da disciplina de Raciocínio Lógico das provas da Polícia Federal (PF) de 2021 para os cargos de Agente, Escrivão e Papiloscopista.
Ressalto que a ordem das questões pode variar de acordo com cada modelo de prova.
Texto para as questões 49, 50 e 51
Para realizar uma operação de busca e apreensão, em duas localidades diferentes, devem ser deslocadas duas equipes, cada uma delas composta por 1 delegado, 1 escrivão e 2 agentes.
Tendo como base essas informações, julgue os itens seguintes.
Questão 49
Questão 49. Se estiverem disponíveis, no momento de formação das equipes, exatamente, 2 delegados, 2 escrivães e 4 agentes, o número de maneiras distintas de se montar as duas equipes seria igual ao número de maneiras de se montar, escolhendo-se entre esses mesmos profissionais, uma única equipe para a realização de uma busca em uma única localidade.
Gabarito: CERTO.
Comentários:
Temos um total de 2 delegados, 2 escrivães e 4 agentes.
Ao escolhermos uma única equipe composta por 1 delegado, 1 escrivão e 2 agentes, o pessoal remanescente é exatamente 1 delegado, 1 escrivão e 2 agentes.
Isso significa que, uma vez escolhida uma única equipe, a segunda equipe já está definida, e é composta pelo delegado remanescente, pelo escrivão remanescente e pelos dois agentes remanescentes. Logo, o número de maneiras distintas de se montar as duas equipes é igual ao número de maneiras de se montar uma única equipe.
Questão 50
Questão 50. Se estiverem disponíveis, no momento de formação das equipes, 3 delegados, 4 escrivães e 6 agentes, o número de maneiras distintas de se montar as duas equipes é superior a 6.500.
Gabarito: ERRADO.
Comentários:
Temos um total de 3 delegados, 4 escrivães e 6 agentes.
O número de maneiras distintas de se montar as duas equipes é dado pelo seguinte produto:

Para montar a primeira equipe, devemos selecionar 1 delegado dentre 3, 1 escrivão dentre 4 e 2 agentes dentre 6. Logo:
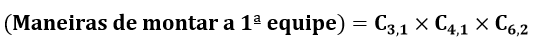
Uma vez definida a primeira equipe, resta-nos 2 delegados, 3 escrivães e 4 agentes. Para montar a segunda equipe, devemos selecionar 1 delegado dentre 2, 1 escrivão dentre 3 e 2 agentes dentre 4. Logo:

Portanto, o número de maneiras distintas de se montar as duas equipes é:

Logo, o número de maneiras distintas de se montar as duas equipes é inferior a 6.500.
Questão 51
Questão 51. Se estiverem disponíveis, no momento de formação das equipes, exatamente, 2 delegados, 2 escrivães e 4 agentes, o número de maneiras distintas de se montar as duas equipes é igual a 4!.
Gabarito: CERTO.
Comentários:
Temos um total de 2 delegados, 2 escrivães e 4 agentes.
O número de maneiras distintas de se montar as duas equipes é:
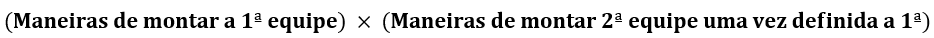
Para montar a primeira equipe, devemos selecionar 1 delegado dentre 2, 1 escrivão dentre 2 e 2 agentes dentre 4. Logo:
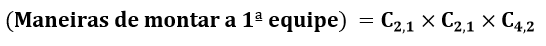
Note que, definida a primeira equipe, o pessoal remanescente é exatamente 1 delegado, 1 escrivão e 2 agentes. Temos, portanto, uma única maneira de montar a segunda equipe.
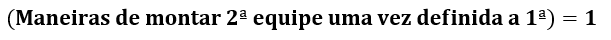
Portanto, o número de maneiras distintas de se montar as duas equipes é:

Logo, o número de maneiras distintas de se montar as duas equipes é igual a 4!.
Texto para as questões 52 a 57
P1: Se a fiscalização foi deficiente, as falhas construtivas não foram corrigidas.
P2: Se as falhas construtivas foram corrigidas, os mutuários não tiveram prejuízos.
P3: A fiscalização foi deficiente.
C: Os mutuários tiveram prejuízos.
Considerando um argumento formado pelas proposições precedentes, em que C é a conclusão, e P1 a P3 são as premissas, julgue os itens a seguir.
Antes de julgarmos os itens da questão, vamos descontextualizar o problema. Considere as proposições simples:
d: “A fiscalização foi deficiente.”
f: “As falhas construtivas foram corrigidas.”
m: “Os mutuários tiveram prejuízos.”
Nesse caso, o argumento apresentado é dado por:
P1: d→~f – “Se [a fiscalização foi deficiente], [as falhas construtivas não foram corrigidas].”
P2: f→~m – “Se [as falhas construtivas foram corrigidas], [os mutuários não tiveram prejuízos].“
P3: d – “A fiscalização foi deficiente.”
C: m – “Os mutuários tiveram prejuízos.”
Descontextualizado o problema, vamos julgar os itens.
Questão 52
Questão 52. O argumento apresentado não é válido.
Gabarito: CERTO.
Comentários:
Para aferir a validade do argumento, vamos utilizar o método da conclusão falsa.
Partir da hipótese de que a conclusão é falsa
Considerando a conclusão falsa, m é F.
Tentar obter ao menos um caso em que todas as premissas sejam verdadeiras mantendo a conclusão falsa
Para a premissa P3 ser verdadeira, d é V.
Para a premissa P1 ser verdadeira, não podemos recair no caso em que a condicional é falsa (V→F). Como o antecedente d é verdadeiro, o consequente ~f deve ser verdadeiro. Logo, f é F.
A partir dos valores já obtidos, a premissa P2 é verdadeira, pois recaímos em um condicional F→V.
Veja que é possível fazer com que todas as premissas sejam verdadeiras mantendo a conclusão falsa. Basta que m seja F, d seja V e f seja F.
Logo, o argumento é inválido, ou seja, não é válido. O gabarito, portanto, é CERTO.
Questão 53
Questão 53. A proposição P2 é equivalente a “Se as falhas construtivas não foram corrigidas, os mutuários tiveram prejuízos”.
Gabarito: ERRADO.
Já vimos que proposição P2 é dada pela condicional f→~m.
Uma equivalência fundamental envolvendo o conectivo condicional é a contrapositiva: p→q ≡ ~q→~p. Para aplicar essa equivalência, devemos realizar o seguinte procedimento:
• Invertem-se as posições do antecedente e do consequente; e
• Negam-se ambos os termos da condicional.
Para o caso em questão, temos:
f→~m ≡ ~(~m) →~f
A dupla negação de uma proposição corresponde à proposição original. Ficamos com:
f→~m ≡ m →~f
A proposição equivalente pode ser descrita por:
m→~f: “Se [os mutuários tiveram prejuízos], [as falhas construtivas não foram corrigidas].”
Veja que o item em questão negou ambos os termos da condicional sem inverter a proposição do antecedente e do consequente.
~f→m: “Se [as falhas construtivas não foram corrigidas], [os mutuários tiveram prejuízos]”.
O gabarito, portanto, é ERRADO.
Questão 54
Questão 54. Caso o argumento apresentado seja válido, a proposição C será verdadeira.
Gabarito: ERRADO.
Note que a questão trata sobre a diferença entre validade dos argumentos dedutivos e verdade das proposições.
Primeiramente, devemos observar que o argumento apresentado não é válido. Mesmo considerando que o argumento é válido, conforme o comando do item, ainda assim não poderíamos dizer que a conclusão C é verdadeira. Isso porque existem três situações em que um argumento pode ser válido:
• Premissas verdadeiras e conclusão verdadeira;
• Premissas falsas e conclusão falsa; e
• Premissas falsas e conclusão verdadeira.
Logo, mesmo que o argumento fosse válido, poderíamos ter a conclusão falsa. O gabarito, portanto, é ERRADO.
Questão 55
Questão 55. A proposição P1 é equivalente a “Não é verdade que a fiscalização foi deficiente e que as falhas construtivas foram corrigidas”.
Gabarito: CERTO.
Vimos que a proposição P1 é dada por d→~f.
A proposição equivalente sugerida pelo enunciado é dada por ~(d∧f).
~(d∧f): “Não é verdade que [(a fiscalização foi deficiente) e (que as falhas construtivas foram corrigidas)]“.
Podemos desenvolver ~(d∧f) por De Morgan. Ficamos com:
~(d∧f) ≡~d∨~f
Temos a disjunção inclusiva ~d∨~f que deve ser comparada com a condicional P1. Devemos, então, transformar essa disjunção inclusiva em uma condicional por meio da equivalência p ∨ q ≡ ~p→q.
Para aplicar essa equivalência, devemos realizar o seguinte procedimento:
• Nega-se o primeiro termo;
• Troca-se a disjunção inclusiva (∨) pela condicional (→); e
• Mantém-se o segundo termo.
Ficamos com:
~d∨~f ≡ ~(~d)→~f
A dupla negação de uma proposição corresponde à proposição original:
~d∨~f ≡ d→~f
Note, portanto, que a proposição sugerida, dada por ~(d∧f), é equivalente a ~d∨~f que, por sua vez, é equivalente a P1, dada por d→~f. O gabarito, portanto, é CERTO.
Questão 56
Questão 56. Uma negação correta da proposição P1 pode ser expressa por: “Se a fiscalização não foi deficiente, as falhas construtivas foram corrigidas”.
Gabarito: ERRADO.
Vimos que a proposição P1 é dada por d→~f.
A negação sugerida pelo enunciado é dada por ~d→f.
~d→f: “Se [a fiscalização não foi deficiente], [as falhas construtivas foram corrigidas].”
Sabe-se da teoria de equivalências lógicas que a negação de uma condicional resulta em uma conjunção dada por meio da seguinte equivalência: ~(p→q) ≡ p∧~q. Somente com esse fato poderíamos marcar o item como ERRADO, pois a negação de uma condicional não resulta em uma condicional.
Para provar formalmente que a negação de d→~f não corresponde a ~d→f, podemos verificar que as tabelas-verdade de ~(d→~f) e ~d→f são distintas.
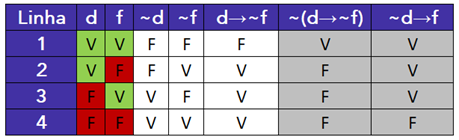
Questão 57
Questão 57. A tabela verdade da proposição condicional associada ao argumento tem menos de dez linhas.
Gabarito: CERTO.
Quando temos um argumento formado pelas premissas P1, P2, P3 e C, a condicional associada ao argumento é dada por:
P1∧P2∧P3 → C
Para o caso em questão, a condicional é dada por:
(d→~f)∧(f→~m)∧d → m
O número de linhas de uma tabela-verdade é dado por 2n, sendo n o número de proposições simples. Para o caso em questão, temos três proposições simples: d, f e m. Logo, o número de linhas da tabela verdade da condicional associada ao argumento é:
2n =23 = 8
Logo, a tabela verdade da proposição condicional associada ao argumento tem menos de dez linhas.
Texto para as questões 58, 59 e 60
Considere os seguintes conjuntos:

e, assim, sucessivamente.
Com base nessas informações, julgue os itens a seguir.
Questão 58
Questão 58. O conjunto P é igual à união infinita dos conjuntos P1, P2, P3, …
Gabarito: CERTO.
Comentários:
Considere um conjunto genérico Px, em que o índice x pode ser 1, 2, 3, …
Note que, genericamente, podemos dizer que o conjunto Px é dado por:
Px = {policiais federais em efetivo exercício no país e que têm até x anos de experiência no exercício do cargo}
Observe que um conjunto de um determinado índice contém todos os conjuntos de índices inferiores. Exemplo:
• P5 contém os conjuntos P4, P3, P2 e P1.
• P8 contém os conjuntos P7, P6, P5, P4, P3, P2 e P1.
Professor, não entendi!
Ok, então vamos mostrar um exemplo mais detalhado.
—–
Exemplo: P3 contém P2 e contém P1. Isso porque:
Em P1, temos policiais com no máximo 1 ano de experiência. Note que todos os policiais que têm no máximo 1 ano de experiência não têm mais do que 3 anos de experiência e, portanto, esses policiais pertencem ao conjunto P3. Isso significa que P1 está contido em P3, ou seja, P3 contém P1.
Em P2, temos policiais com no máximo 2 anos de experiência. Note que todos os policiais que têm no máximo 2 anos de experiência não têm mais do que 3 anos de experiência e, portanto, esses policiais pertencem ao conjunto P3. Isso significa que P2 está contido em P3, ou seja, P3 contém P2.
—–
Voltando ao problema, a união infinita dos conjuntos P1, P2, P3… pode ser escrita informalmente por:
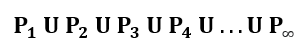
Note que o conjunto de maior índice (infinito), P∞, contém todos os outros conjuntos de índice inferior. Isso significa que:
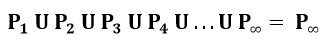
Note que o conjunto P∞ pode ser entendido por:
P∞= {policiais federais em efetivo exercício no país e que têm até infinitos anos de experiência no exercício do cargo}
Veja que os policiais que têm até infinitos anos de experiência corresponde à totalidade dos policiais. Isso significa que:
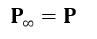
Logo:
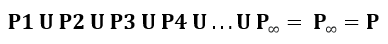
Portanto, o conjunto P é igual à união infinita dos conjuntos P1, P2, P3, …
Questão 59
Questão 59. P2 é subconjunto de P1
Gabarito: ERRADO.
Comentários:
Em P1, temos policiais com no máximo 1 ano de experiência. Em P2, temos policiais com no máximo 2 anos de experiência.
Note que todos os policiais que têm no máximo 1 ano de experiência não têm mais do que 2 anos de experiência e, portanto, esses policiais pertencem ao conjunto P2. Isso significa que P1 está contido em P2, ou seja, P1 é subconjunto de P2. Logo, a questão erra ao dizer que P2 é subconjunto de P1.
Questão 60
Questão 60. Escolhendo-se aleatoriamente um integrante do conjunto P, a probabilidade de ele ter entre dois e três anos de experiência no exercício do cargo é dada por n(P2-P3)/n(P3), em que n(X) indica o número de elementos do conjunto X e P2-P3 é o conjunto formado pelos indivíduos que estão em P2 mas não estão em P3
Gabarito: ERRADO.
Comentários:
Escolhendo-se aleatoriamente um integrante do conjunto P, isto é, escolhendo-se aleatoriamente um integrante dentre todos os policiais federais em efetivo exercício no país, a probabilidade de ele ter entre dois e três anos de experiência no exercício do cargo é dada por:

Em P3 temos policiais com no máximo 3 anos de experiência. Já em P2 temos policiais com no máximo 2 anos de experiência. P3 – P2 são os policiais com experiência entre 2 e 3 anos. Logo:

A questão erra ao afirmar que a probabilidade é n(P2-P3)/n(P3).
Considerações finais
Esse é o nosso gabarito extraoficial da disciplina de Raciocínio Lógico. Espero que tenham alcançado um bom desempenho. Até a próxima!