Saiba tudo sobre o losango

Entenda tudo sobre o losango.

Olá pessoal, tudo bem?

Atualmente muitas questões de Matemática em concursos precisam explorar os recursos visuais para serem resolvidas. Certamente algumas delas podemos associar a figuras já conhecidas e alcançar o resultado por meio de aplicação de suas propriedades.

Uma dessas figuras que iremos analisar aqui é o losango, um quadrilátero muito presente nas imagens do nosso dia a dia. Por isso, vamos descobrir as principais características dessa figura plana.

O que é um quadrilátero?

Quadriláteros são figuras planas que possuem quatro lados. Quadrados e retângulos são bons exemplos desse tipo de figura facilmente identificados pelas pessoas, mas vamos estender essa visão para os outros tipos.

Os quadriláteros podem ser classificados de acordo com a relação entre os tamanhos dos lados (se são iguais ou não), seu alinhamento em relação lados opostos (se são paralelos ou não) e com relação aos ângulos formados. Então, vejamos as principais classificações de quadriláteros:

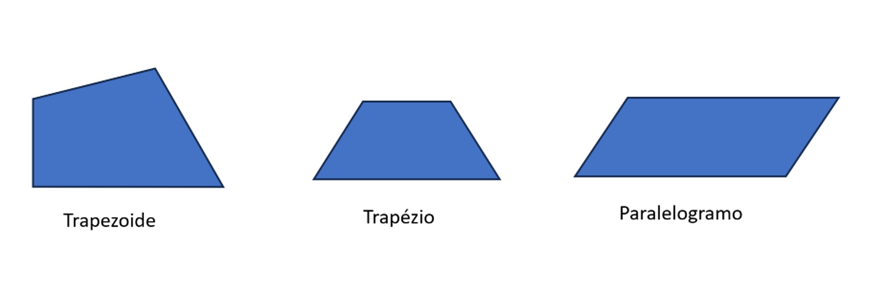
Trapezoide: não possui nenhum lado paralelo.

Trapézio: possui um par de lados paralelos e outro não paralelo.

Paralelogramo: possui dois pares de lados paralelos.

O paralelogramo ainda pode ser:

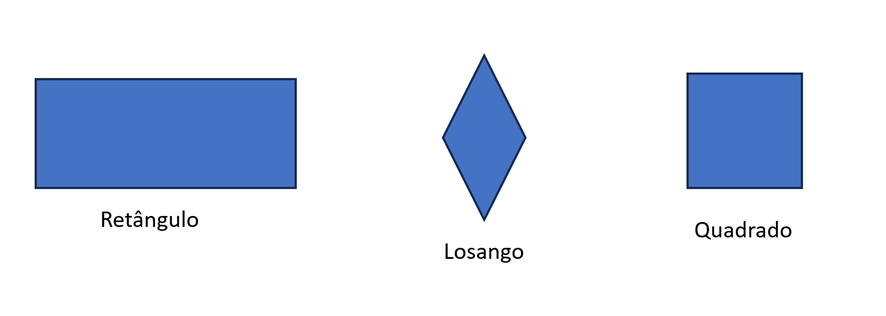
Retângulo: possui todos os ângulos retos (medindo 90 °).

Losango: possui todos os lados iguais.

Quadrado: losango e retângulo ao mesmo tempo, ou seja, todos os lados e ângulos iguais.

Quais as características de um losango?

Conforme já exposto, o losango é um quadrilátero que possui todos os lados iguais. Embora esse seja seu diferencial, podemos listar algumas características comuns a outras figuras.

Por ser quadrilátero, o losango:

• Possui duas diagonais, que são seguimentos que vão de um vértice (“ponta”) a outro sem sobrepor a um dos lados.

• Possui a soma dos seus ângulos internos igual a 360°.

Por ser paralelogramo, o losango:

• Possui dois pares de ângulos iguais. Os ângulos iguais são opostos entre si, ou seja, são os ângulos que ficam um de frente para o outro.
• Possui área calculável pela fórmula dos paralelogramos: Área = base x altura.
• Possui lados opostos paralelos entre si.
• Possui ângulos adjacentes (formados pelo mesmo lado) suplementares (cuja soma resulta em 180°).

Além disso, o losango:

• Possui perímetro igual ao quádruplo da medida de um lado: Perímetro = 4 x L.
• Possui diagonais que se cruzam exatamente no ponto médio delas e, por isso, também o ponto médio do losango.
• Possui diagonais que dividem o losango em quatro triângulos retângulos (com um ângulo reto) congruentes (com as mesmas medidas).

Área do losango

Conforme citado, uma das formas de se calcular área do losango é utilizando a fórmula dos paralelogramos (Área = base x altura), considerando a base como sendo um dos lados e a altura a distância perpendicular entre os lados paralelos. Mas também há outras formas.

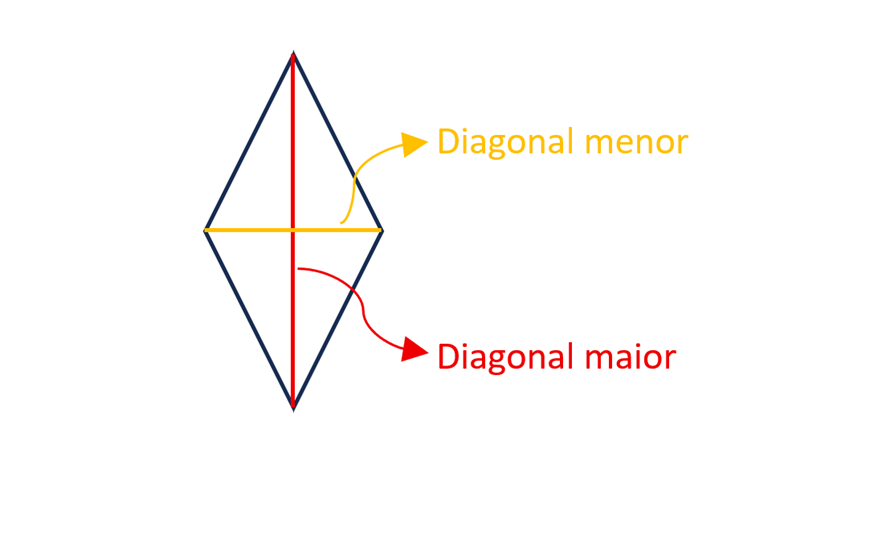
Certamente, a fórmula mais difundida é através das diagonais:

A = D x d / 2

Onde a A é a área, D é a diagonal maior e d é a diagonal menor.

Além disso, quando apenas as medidas do lado e de um ângulo são conhecidas, pode ser utilizada a fórmula:

Afinal, como cai em concurso?

Geralmente as questões mais numerosas sobre losango envolvem cálculo de área, mas observe essa questão diferente cobrada pela banca VUNESP em 2018:

Questão 1

Em um losango, os ângulos opostos são congruentes. A figura representa um losango, sendo que as incógnitas x e y representam valores em graus.



A soma x + y vale

Alternativas

A 24°

B 40°

C 56°

D 72°

E 88°

Resposta:

De imediato podemos afirmar que 3y = x, já que são ângulos opostos e nos paralelogramos possuem a mesma medida. Além disso, nos paralelogramos a soma dos ângulos adjacentes (ângulo maior + ângulo menor) resulta em 180°. Assim vejamos:

5x – 6y + 12 + 3y = 180 (soma do ângulo maior com o que mede 3y)

Já que afirmamos que 3y e x são iguais, podemos substituir o x por 3y e resolver a equação.

5.3y – 6y + 12 + 3y = 180

15y – 6y + 12 + 3y = 180

12y + 12 = 180

12y = 180 – 12

12 . y = 168

y = 168/12

y = 14

Adotando que x = 3y e que y = 14, obtemos que x = 42. A questão pediu o resultado de x + y, ou seja, 42 + 14 = 56. Alternativa C

Vamos em seguida para outra questão envolvendo losango cobrada pela banca Instituto Excelência em 2018.

Questão 2

As diagonais de um losango medem 12 cm e 14 cm. Se a medida da diagonal menor diminuir 2 cm, quantos centímetros devemos aumentar a diagonal maior para que o losango permaneça com a mesma área?

Alternativas

A 3,6cm.

B 2,8 cm.

C 1,4cm.

D Nenhuma das alternativas.

Antes de mais nada podemos adotar o cálculo da área do losango inicial pela fórmula das diagonais:

A = D . d / 2

A = 12 . 14 / 2

A = 84 cm²

Sabemos que precisamos diminuir 2 cm da diagonal menor, por isso passa a medir 10 cm. Na diagonal maior, precisamos acrescentar um valor que vamos chamar de x, medindo assim 14 + x. Assim, mantendo a mesma área, teremos:

A = D . d / 2

84 = (14 + x) . 10 / 2

84 = (14 + x) . 5

84 : 5 = 14 + x

16,8 = 14 + x

16,8 – 14 = x

2,8 = x

Alternativa B.

Considerações finais sobre o losango

O losango é uma figura bem comum no nosso dia a dia, podendo ser associada principalmente a logomarcas, formatos de pipas e etc. Além disso, sua presença também se estende às questões de concursos de diversas bancas.

Assim, dominar a interpretação e as características dessa figura pode ser decisivo na hora de conseguir aquele pontinho a mais em Matemática. Estude o conteúdo com calma e pratique com questões anteriores sempre que possível.

Bons estudos!!!

Quer saber quais serão os próximos concursos? 

Confira nossos artigos! 

Concursos abertos 

Concursos 2026