Resumo sobre Arranjo Combinação e Permutação

Fala, estrategistas! Vamos fazer um Resumo sobre Arranjo, Combinação e Permutação que são conceitos fundamentais em matemática.

Esses conceitos são frequentemente utilizados em diversas áreas, como estatística, probabilidade e teoria dos conjuntos. 

O Arranjo, Combinação e Permutação servem para calcular o número de maneiras diferentes que um conjunto de objetos pode ser organizado ou selecionado em um universo amostral. 

Aprendendo sobre Arranjo, Combinação e Permutação

Cada um desses conceitos tem suas próprias regras e fórmulas específicas. Vamos ver Arranjo, Combinação e Permutação em detalhes e entender como aplicam-se em diferentes situações.

FATORIAL

Definimos como o fatorial de n (simbolizado por n!) ao produto do n primeiros números inteiros positivos. Caso n = 0, definiremos 0! =1. Dessa forma, teremos:

n! = n .(n-1) . (n-2) . (n-3)

Veja o exemplo:

5! = 5x4x3x2x1 = 120

PERMUTAÇÕES

Para permutar elementos os trocamos de posições. A forma de calcular as possibilidades que podemos realizar com esses elementos dependerá da natureza dos elementos permutados. 

PERMUTAÇÕES SIMPLES

Uma permutação de n objetos distintos é qualquer agrupamento ordenados desses objetos, de modo que, se denominarmos Pn  o número das permutações simples dos n objetos, então:

Pn  = n!

Vamos imaginar que dispomos de  n objetos distintos para serem colocados em fila, ocupando n posições. 

Por meio do  Princípio Multiplicativo, temos n objetos para ocupar a primeira posição. Ocupada a 1a posição com um objeto, a segunda posição pode ser ocupada por qualquer um dos n – 1 objetos restantes, pois um objeto já está colocado na posição de número 1.

Ocupada a segunda posição, a terceira posição pode ser ocupada por qualquer um dos n – 2 objetos restantes. 

Dessa forma, repetindo esse raciocínio até o último objeto, restará para ele a última posição da fila. Logo, pelo Princípio Multiplicativo, teremos:

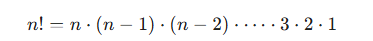
Essa sequência é exatamente o mesmo que escrever  n!

Exercício de aplicação

De quantas maneiras diferentes 5 amigos podem se sentar em um banco de cinema com 5 lugares?

Imagine os 5 assentos do cinema:

[ Assento 1 ] [ Assento 2 ] [ Assento 3 ] [ Assento 4 ] [ Assento 5 ]

• Para o 1º assento: Você tem 5 amigos disponíveis para escolher.
• Para o 2º assento: Como um já sentou, restam 4 amigos.
• Para o 3º assento: Restam 3 amigos.
• Para o 4º assento: Restam 2 amigos.
• Para o 5º assento: Resta apenas 1 amigo.

Vamos fazer o Cálculo

Multiplicamos as possibilidades de cada vaga (o que chamamos de 5!).

5! = 5x4x3x2x1 = 120 

Assim, sabemos que há 120 possibilidades desses amigos sentarem em um banco de cinema.

ARRANJOS

Nas Permutações trocamos de posição todos os elementos de uma sequência de objetos qualquer. 

No Arranjo, geralmente, fazemos uma permutação de apenas uma parte dos objetos dados, onde a ordem dos mesmos também influencia na disposição dos elementos.

Quando temos um arranjo em que estamos interessados na troca de posição de todos os elementos, esse arranjo é uma permutação.

ARRANJOS SIMPLES

Considere um conjunto com  n elementos distintos. 

Qualquer sequência de p desses elementos (todos distintos) denomina-se Arranjo Simples (0 ≤ p ≤ n, com n e p naturais). 

Dizemos arranjo simples de n elementos tomados  p a p, e simbolizamos por An ,p.

Esse arranjo simples calcula-se da seguinte forma:

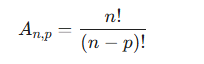
Exercício aplicado

Em uma competição de natação com 8 atletas, de quantas maneiras diferentes podem ser formados os pódios (1º, 2º e 3º lugares)?

Por que é Arranjo? Porque a Ordem importa:

Se o atleta A chega em 1º e o B em 2º, é um resultado diferente de B em 1º e A em 2º.Subgrupo: Temos 8 atletas, mas apenas 3 ocuparão o pódio.

Imagine as 3 posições do pódio:[ 1º Lugar ] [ 2º Lugar ] [ 3º Lugar ]

Para o 1º lugar, temos 8 possibilidades de atletas.

2º lugar, restam 7 possibilidades (pois um já ganhou o ouro).

3º lugar, restam 6 possibilidades.

8x7x6 = 336 possibilidades. Vamos fazer pela fórmula agora:

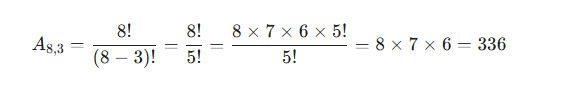
ARRANJOS COM REPETIÇÃO

Considere um conjunto com  n elementos distintos. 

Qualquer sequência de  p desses elementos é chamada de Arranjo com repetição (0 ≤ p ≤ n, com  n  e  p  naturais). 

Os elementos podem ser distintos ou não, isto é, pode haver elementos repetidos.

Dizemos arranjo com repetição de n elementos tomados  p  a  p, e simbolizamos por ARn, p.

Esse arranjo com repetição calcula-se da seguinte forma:

AR_n,p = n^P

Exercício aplicado

Quantas senhas de 3 dígitos podem ser criadas utilizando apenas os algarismos 1, 2, 3, 4 e 5?

Por que é Arranjo com Repetição?Ordem importa: A senha “123” é diferente da senha “321”.

Repetição permitida: O enunciado não diz que os algarismos devem ser “distintos”. Logo, a senha “111” ou “221” é perfeitamente válida.

Temos 3 espaços para preencher: [ _ ] [ _ ] [ _ ]

Para o 1º dígito: Temos 5 opções (1, 2, 3, 4 ou 5).

2º dígito: Como pode repetir, continuamos tendo 5 opções.

Para o 3º dígito: Continuamos tendo 5 opções.

Cálculo: 5x5x5 = 125 senhas diferentes

Vamos usar a fórmula para o cálculo

A fórmula para arranjo com repetição é AR _n,p = n^P,  

^Onde: 

• ^{n = 5 ( número de elementos disponíveis)}
• ^{p = 3 ( número de posições a preencher)}
• 5 ^{3 = 125}

COMBINAÇÕES

As combinações podem ser simples e também com repetição (também chamadas de combinações completas).

COMBINAÇÕES SIMPLES

Considere um conjunto com  n elementos distintos. Qualquer subconjunto formado por de p desses elementos (todos distintos) denomina-se de Combinação Simples (0 ≤ p ≤ n, com n e p naturais).

Dizemos combinação simples de n elementos tomados p a p, e simbolizamos por Cn,p

Essa combinação simples calcula-se da seguinte forma:

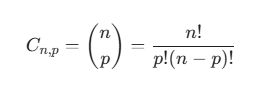
Exercício aplicado de Combinação Simples

Uma pizzaria oferece 10 ingredientes diferentes. De quantas maneiras um cliente pode escolher 3 ingredientes para montar sua pizza personalizada?

Por que é Combinação?A ordem não importa: Se você escolher (Queijo, Presunto e Azeitona), a pizza será a mesma se você escolher (Azeitona, Queijo e Presunto). O conjunto de ingredientes final é o que conta.

1. Total de elementos (n): 10 ingredientes.
2. Elementos escolhidos (p): 3 ingredientes.

Utilizando a fórmula:

 O cliente pode montar a pizza de 120 maneiras diferentes.

Exercício aplicado de Combinação Composta

Uma sorveteria possui 4 sabores de sorvete: Chocolate, Morango, Baunilha e Limão. De quantas maneiras diferentes um cliente pode comprar um pote com 3 bolas de sorvete?

Por que é Combinação com Repetição? A ordem não importa: Um pote com (Chocolate, Chocolate, Limão) é o mesmo que (Limão, Chocolate, Chocolate).

Repetição permitida: O cliente pode querer 3 bolas do mesmo sabor (ex: 3 de Morango).

Existem 20 combinações diferentes de potes de sorvete.

Encerramos por aqui nosso artigo. Esperamos que você tenha compreendido a importância do Arranjo, Permutação e Combinação e seu uso na Matemática.

Por hoje é isso, pessoal!

Abraços e até a próxima.

Bárbara Rocha

Assista as nossas aulas para aprofundar-se nos temas e obter sucesso na sua aprovação :)

ASSINE AGORA – Assinaturas

Assine agora a nossa Assinatura Anual e tenha acesso ilimitado* a todos os nossos cursos.

Fique por dentro de todos os concursos:

Concursos abertos

Concursos 2026