Resumo das Variáveis Aleatórias Contínuas ISS-BH – Estatística

Olá, pessoal. Tudo certo? No artigo de hoje veremos o Resumo das Variáveis Aleatórias Contínuas ISS-BH.

Tópicos que serão vistos:

• Conceitos Gerais
• Função de distribuição acumulada
• Distribuição Uniforme
• Distribuição exponencial
• Distribuição normal

Preparado (a)? Vamos lá.

Conceitos Gerais

Iniciemos o Resumo das Variáveis Aleatórias Contínuas ISS-BH pelos conceitos gerais/iniciais.

Variáveis aleatórias contínuas são aquelas que podem assumir quaisquer valores dentro de um intervalo, assim podemos dizer que elas não podem ser enumeradas (contadas), como por exemplo, a altura.

Nesse caso da altura, uma pessoa pode ter 1,80m de altura, entretanto se melhorar a precisão poderia ser 1,802m, ou seja, a probabilidade de um valor específico dentro de um intervalo é nula.

Assim, ao invés de utilizarmos uma função de probabilidade f (x) = P (X = x) como nas variáveis discretas, utilizamos uma função densidade de probabilidade (f.d.p), para trabalhar com intervalos.

Condições da função densidade de probabilidade:

• Uma probabilidade qualquer nunca é negativa
• A probabilidade associada a todo o Espaço Amostral é igual a 100%

Nesse sentido, a probabilidade será dada pela área da função.

Exemplo: (VUNESP/2014 – TJ-PA) Uma variável aleatória contínua tem uma função de probabilidade dada por f(x) = K.x, válida apenas no intervalo 1≤ x ≤ 2. Fora desse intervalo f(x) = 0. De acordo com isso o valor de K é:

Integral de k.x dx é igual a

 (k/2) .  x² = 1

Tendo como intervalo de 2 e 1, assim  

k/2 . (2² – 1²) = 1

Logo,

k/2 . 3 = 1

Assim,

K = 2/3

Função de distribuição acumulada

A função de distribuição acumulada basicamente é a probabilidade acumulada desde o início até o ponto indicado.

Vamos ver por meio de um exemplo, mas antes disso vejamos as características da função acumulada.

Características

• FA é não decrescente, pois as probabilidades são sempre somadas.
• Por ser uma probabilidade, a f.d.a. assume valores entre 0 e 1

Exemplo: (FCC/2012 – Analista Judiciário do TRF da 2ª Região) Uma variável aleatória contínua tem função densidade de probabilidade dada por:

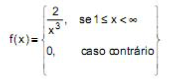
Se F(x) é a função de distribuição de X, então F(2) é igual a:

Primeiro deve-se integrar 2/x³,

= 2 . x^-2 / -2

= -x^-2

= -1/x²

E adotando os limites de 1 (limite inferior) até o ponto desejado (2).

F(2) = (-1/2²) – (-1/1²)

F(2) = -1/4 + 1

F(2) = 3/4

Medidas de posição central

Sabemos que a mediana divide em duas partes iguais a distribuição, assim devemos igualar a f.d.p em 50%

Exemplo: F(x) = 8x²

8x² = 1/2

x² = 1/16

x = sqrt (1/16)

x = 1/4

A moda é o valor correspondente a maior frequência/probabilidade.

É possível verificar graficamente, mas na impossibilidade temos que derivar a função.

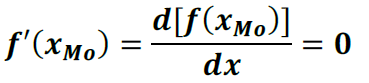
Exemplo: (FCC/2011 – Analista Judiciário do TRT da 1ª Região) Considere a variável aleatória contínua X com função densidade de probabilidade dada por:

Valor da moda será:

f (x) = 12x² – 12x³

Derivando a função

12 . 2 x¹ – 12 . 3x²

24x – 36x²

Igualando a 0

24x – 36x² = 0

Agora podemos simplificar por /12x

2 – 3x = 0

Logo, a moda será:

x = 2/3

Tanto a média quanto a variância podemos calcular a partir das integrais.

• Esperança Matemática

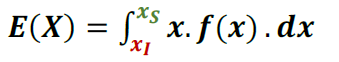
• Variância

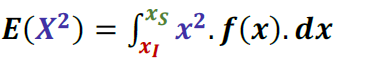
Distribuição Uniforme

Dando continuidade ao Resumo das Variáveis Aleatórias Contínuas ISS-BH, vejamos sobre a Distribuição uniforme.

A Distribuição uniforme apresenta o mesmo valor de probabilidade para qualquer valor.

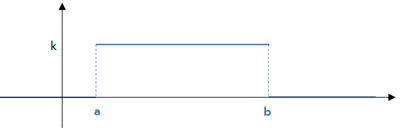
Assim, para calcular um intervalo em uma distribuição uniforme basta calcular a área do período desejado.

Exemplo: (FGV/2017 – IBGE) Uma variável aleatória contínua X é uniformemente distribuída no intervalo real [0, 50]. A probabilidade de que X seja maior do que 20 é igual a:

K x (50 – 0) = 1

K x 50 = 1

K = 1/50

Para a área desejada

P = (50 – 20) x 1/50

P = 30 x 1/50

P = 0,6

• Esperança Matemática

Como estamos falando de um retângulo, o valor da média será exatamente no meio

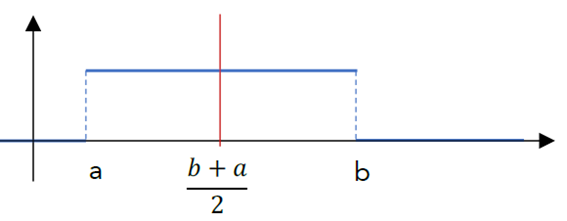
• Variância

Já a variância temos:

V (X) = (b – a)² / 12

Distribuição exponencial

A distribuição exponencial taxa de falha constante e comporta-se, como o nome sugere, de forma exponencial.

Função densidade de probabilidade (f.d.p.)

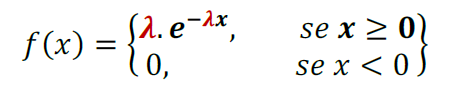
Ainda, podemos calcular a probabilidade para um X maior do que algum valor, ou em outros termos, a função de distribuição acumulada no ponto.

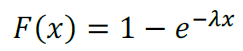
• Esperança matemática

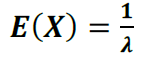
• Variância

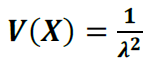
Exemplo: FGV – Analista Judiciário (TJ AL)/Apoio Especializado/Estatística/2018 

Suponha que o tempo de espera para a marcação de uma 1ª audiência nas varas de família de um tribunal seja uma variável aleatória que depende do número de novas ações, seguindo uma distribuição exponencial com média de 2,5 meses.

Então, trabalhando com  e^−0,4 = 2/3 , probabilidade de que uma 1ª audiência seja marcada para mais do que 2 meses depois é igual a aproximadamente:

F(2) = 1 – (2/3)²

F(2) = 1 – 4/9

F(2) = 5/9

Assim, a chance de ser marcada até 2 meses é de 5/9

Então a chance para depois de 2 meses será o complemento

P = 1 – 5/9

P = 4/9

Distribuição Normal

Para finalizar o Resumo das Variáveis Aleatórias Contínuas ISS-BH, vamos revisar a Distribuição Normal.

A Distribuição normal (gaussiana) é a distribuição mais cobrada entre as contínuas, então é necessário uma atenção redobrada.

A distribuição pode ser demonstrada graficamente:

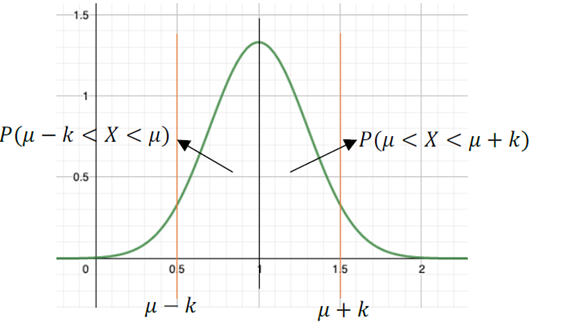
Para que possamos encontrar o valor da probabilidade devemos consultar em uma tabela (a maioria dos exercícios fornece por meio de dados), entretanto antes devemos transformar os valores do exercício para valores normalizados.

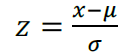
Exemplo: (FGV/2016 – IBGE) Sabe-se que as notas de uma prova têm distribuição Normal com média = 6,5 e variância = 4 . Adicionalmente, são conhecidos alguns valores tabulados da normal-padrão.

Z(1,3 ) ≅ 0,90;  Z(1,65) ≅ 0,95; Z(1,95 ) ≅ 0,975; Onde, Z é a função distribuição acumulada da

Normal Padrão.

Considerando-se que apenas os 10% que atinjam as maiores notas serão aprovados, a nota mínima para aprovação é:

1,3 = x – 6,5 / sqrt 4

1,3 . 2 = x – 6,5

X = 9,1

Considerações Finais

Pessoal, chegamos ao final do Resumo das Variáveis Aleatórias Contínuas ISS-BH. Espero que o artigo tenha sido efetivo para seu aprendizado.

Obviamente trata-se de um resumo apenas com os pontos principais da matéria, tendo outros temas correlacionados como a Desigualdade de Chebyshev, Distribuição t-Student entre outros, assim não deixe de acompanhar as aulas para o aprofundamento necessário.

Ainda, ressaltamos mais uma vez a importância de praticar por exercícios, assim faça muitas questões pelo nosso sistema de questões.

Sistema de Questões (SQ) – Estratégia Concursos

Gostou do artigo? Não deixe de seguir

https://www.instagram.com/resumospassarin/

Cursos e Assinaturas

Até mais e bons estudos!