Como entender os Teoremas da Probabilidade

Facilitamos uma difícil matéria: Estatística. Vamos entender os Teoremas da Probabilidade e auxiliar na memorização de suas fórmulas.

Olá pessoal, tudo bem?Hoje, vamos tentar explicar esses teoremas com lógica e com alguns macetes para que o estudante consiga gravá-las ou entendê-las e não dependa de mnemônicos ou outros métodos de memorização.

Para entender as dicas desse texto é muito importante que o aluno conheça os conceitos de conjuntos, pois eles serão a base para compreendermos probabilidade. Utilizaremos diversas imagens de conjuntos para ilustrar as fórmulas e tentar dar um sentido a cada uma delas.

Estudaremos as seguintes fórmulas:

• Probabilidade da união de A com B – P(AUB);
• Probabilidade da Intersecção de Eventos mutuamente;
• Teorema de Bayes – Teorema da probabilidade condicionada;
• Probabilidade da Intersecção de eventos independentes.

Probabilidade da união de A com B

Iniciamos estudando a probabilidade da união de A com B (AUB) e o porquê de ela se dar pela seguinte fórmula:

 P (A U B) = P(A) + P(B) – P(A∩B)

É uma fórmula de difícil memorização pois existe a retirada da intersecção de P(A) com P(B). Vamos entender por que é necessário retirar essa Intersecção:

Iniciamos definindo dois conjuntos: temos os conjuntos A e B que vamos representar em círculos:

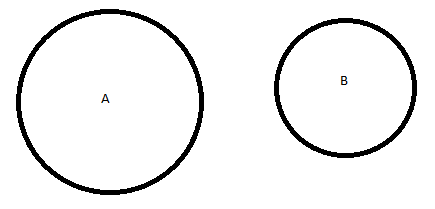
Nesse momento, A e B não tem nenhum termo em comum (já que não se cruzam). Isto é, tudo que existe em A não existe em B e vice-versa.

Nesse exemplo, como dito, todos os números que apareceriam em A nunca apareceriam em B e vice-versa. Para ilustrar o exemplo acima, podemos supor um universo que chamaremos de U que conteria todos os números de 1 a 10 em que A e B estariam contidos.

Esse Universo U seria um conjunto com todos os números de A mais todos os números de B e ainda todos os números que A e B não possuam. Vamos visualizar:

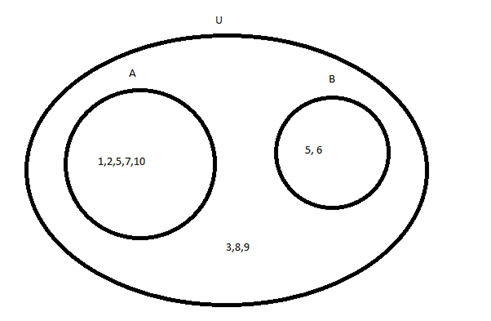
Veja que U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, A= {1, 2, 7, 10} e B= {5, 6}. Os números 3, 8 e 9 não pertencem a nenhum subconjunto de U, estão “soltos”. Tendo entendido isso, podemos também representar U por U = {A, B, 3, 8, 9}, já que ele é a soma dos três itens.

Seguindo com o entendimento de conjuntos para entender os Teoremas da Probabilidade

Para continuar entendendo conjuntos, vamos esquecer os números colocados nos exemplos anteriores e começarmos um novo exemplo utilizando novos valores.

Apresentamos uma intersecção entre A e B:

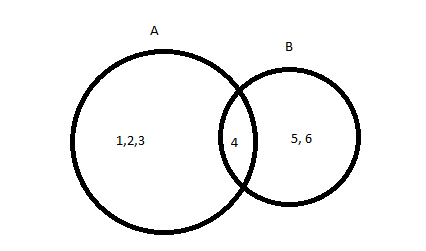
Vemos que A = {1, 2, 3, 4} e B= {4, 5 ,6}, ou seja, há intersecção entre A e B do número 4.

Vamos fazer duas operações com esses conjuntos: A+B e AUB:

A+B = = {1, 2, 3, 4, 4, 5 ,6}

AUB = {1, 2, 3, 4, 5 ,6}

Perceba duas coisas:

• A+B é diferente de AUB.
• Em A+B o item 4 aparece duas vezes, mas o que queremos na união é a junção dos itens A e B sem a repetição da intersecção.

Entendendo a fórmula da União propriamente dita: (AUB)

Para a união de A com B do exemplo anterior, temos que encontrar tudo que existe em A e B sem repetir os termos da intersecção. Desenhando isso, para facilitar, teremos a seguinte área pintada:

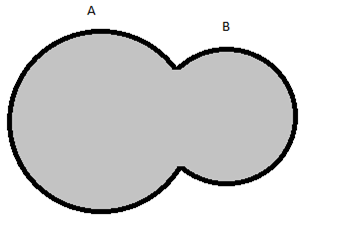
A área em cinza é o equivalente a AUB= {1,2,3,4,5,6}.

Acontece que, como demonstrado anteriormente, quando somamos A com B ao invés de fazermos a união deles, ficamos com A+B = {1,2,3,4,4,5,6}. A+B pode ser representado pela figura abaixo:

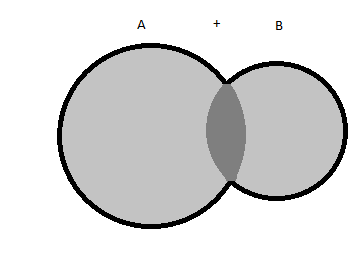
Note que a parte onde há o número 4 do exemplo está mais escura. Isso acontece, pois ela foi adicionada duas vezes (A+B = = {1, 2, 3, 4, 4, 5 ,6}) . Esse 4 é exatamente a intersecção de A com B – (A ∩ B).

Dessa maneira, para encontrarmos a união de A com B –> (AUB) temos que retirar essa intersecção para que tenhamos o resultado final desejado:

Temos o seguinte raciocínio:

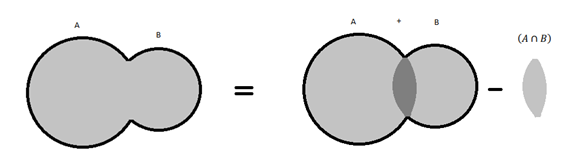
A figura representa:

(A U B) = A + B – (A∩B)

Por uma das propriedades das probabilidades, podemos colocar P em todos os lados da equação e ela continua verdadeira:

(A U B) = A + B – (A∩B)

Colocando P em todos os itens:

P (A U B) = P(A) + P(B) – P(A∩B)

Sendo assim, a probabilidade da união de A com B segue exatamente a mesma fórmula da união de A co B. Grave isso!

Com essa explicação, fica muito fácil de memorizar a fórmula e conseguimos finalmente entender a razão de ela existir.

Eventos mutuamente exclusivos tem intersecção igual a conjunto vazio

Continuando a entender os Teoremas da Probabilidade, seguimos com eventos mutuamente exclusivos, que são eventos que seguem a seguinte lógica: quando um acontece o outro nunca acontece.

Por exemplo: estar acordado, significa que não se está dormindo. O grupo de pessoas acordadas e dormindo é mutuamente exclusivo (Sonâmbulo não conta, rs).

Seguindo a lógica dos conjuntos: se alguém é A, nunca será B e vice-versa. Desse modo, qual pode ser a única intersecção de A com B? Apenas o conjunto vazio (nunca confunda conjunto vazio com o número 0. Eles são coisas muito diferentes).

Uma curiosidade sobre eventos independentes x eventos mutuamente exclusivos:

Perceba que eventos independentes e eventos mutuamente exclusivos não são equivalentes! Os conjuntos mutuamente exclusivos possuem dependência enquanto os independentes não a possuem.

Exemplo:

• Eventos mutuamente exclusivos: Alguem não pode estar acordado e dormindo ao mesmo tempo. Se um for verdade, o outro NECESSARIAMENTE é falso.
• Eventos independentes: gostar de chocolate e ter olho castanho. São duas coisas absolutamente independentes.

Teorema de Bayes – Vamos entender os Teoremas da probabilidade condicionada

Vamos agora tentar entender uma fórmula que é bastante difícil para se decorar, mas que, uma vez entendida, nunca mais é esquecida: a fórmula do Teorema de Bayes, que diz o seguinte:

P(A|B) = P (A∩B) /P(B)

O que esses símbolos significam? Matematicamente, lemo-los da seguinte maneira:

P(A|B) = P (A∩B) /P(B) = A probabilidade de A tal que B é igual a probabilidade da Intersecção de A com B, divido pela probabilidade de B.

Esse “tal que B”, traduzindo para o português comum significa: A probabilidade de A ser verdadeiro tal que B seja verdadeiro.

Desse modo, quando começamos uma formula dessas, já temos uma resposta. Sabemos que B é verdadeiro para que atinjamos o P(A|B). Grave isso!

Utilizando um exemplo matemático

Vamos iniciar nosso exemplo com probabilidades condicionais, isto é, probabilidades que influenciam umas às outras. Observe os seguintes conjuntos:

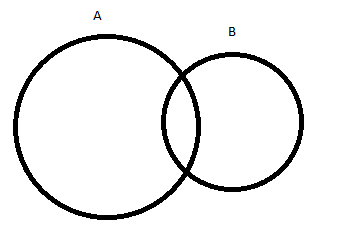
Em P(A|B) já sabemos que B tem que ser verdade para que a condição seja satisfeita. Vamos pintar de verde tudo que é condicionado a ser verdade:

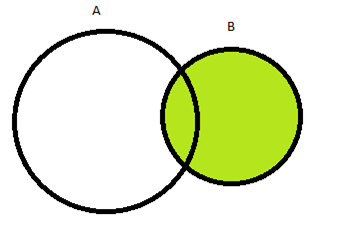
Agora queremos saber qual a probabilidade de A ser verdadeiro quando B é verdadeiro.

Bom, se B tem que ser verdadeiro para atingirmos nossa condução, nós podemos excluir tudo que não está dentro do círculo de B. Então, necessariamente o que nos sobra em nosso universo de possibilidades é apenas onde B é verdadeiro. Ficamos com o seguinte desenho:

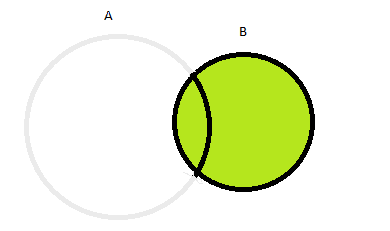
Obs. Mantivemos o “fantasma” do conjunto A para visualização do desenho, mas ele não está mais sendo considerado.

Vamos pintar agora a intersecção entre A e B para diferenciarmos os dois:

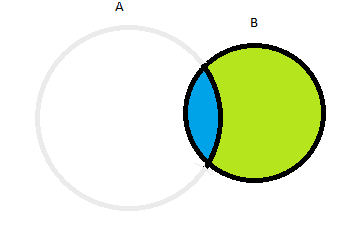
Perceba que:

• Na parte em verde B é verdadeiro, mas A não é verdadeiro
• Na parte em azul, A e B são verdadeiros

Para não nos esquecermos de que na intersecção A e B são verdadeiros, vamos fazer o contorno de B todo em verde:

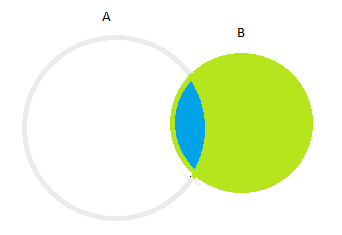
Voltamos à formula:

P(A|B) = P (A∩B) /P(B)

Vamos entender finalmente a fórmula: Queremos a probabilidade de A ser verdadeiro desde que B seja verdadeiro, desse modo o nosso “universo de possibilidades” passa a ser apenas o círculo em verde (B).

Já que nosso universo de probabilidades é apenas o círculo verde e queremos a probabilidade de A ser verdadeiro, apenas a parte de A que também está em B pode fazer parte da nossa condição. Essa parte é a intersecção de A com B -> P (A∩B)

Desse modo fica bastante simples para entendermos a fórmula. Fique coma seguinte imagem para imprimir:

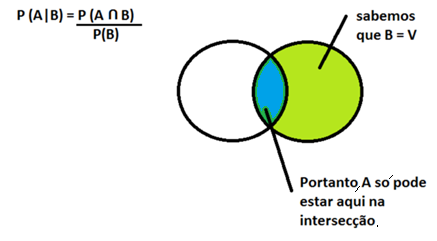
Um exemplo para clarear:

Supondo que A seja a probabilidade de chover e B, a probabilidade de termos um dia ensolarado.

Sabemos que pode sim haver chuva em dia ensolarado, mas há uma dependência entre os dois (em dias ensolarados não se costuma ter chuvas).

Se quisermos saber P (Chuva| dia ensolarado) queremos saber a probabilidade de chover enquanto faz sol, ou seja, já supondo de antemão que o dia está ensolarado.

Ficamos com a seguinte fórmula

P (Chuva| dia ensolarado) = P (Chuva ∩ Dia ensolarado) /P (dia ensolarado)

Intersecção de eventos independentes

Continuando a entender os Teoremas da Probabilidade, suporemos agora dois eventos independentes A e B

Para isso ser verdadeiro, tudo pode acontecer entre A e B:

• A pode ser verdadeiro e B falso,
• B pode ser verdadeiro e A falso,
• A e B podem ser verdadeiros ou
• A e B serem falsos

Fica claro que as probabilidades de A e B são independentes.

Seguindo o Teorema de Bayes para encontrarmos P(A|B), temos que encontrar a probabilidade de A ser verdadeiro apenas quando B é verdadeiro. Oras, Se A independe sempre de B, B não influencia a probabilidade de A.

Desse modo, a probabilidade de A ser verdadeiro quando B for verdadeiro é a mesma probabilidade de A ser verdadeiro quando B é falso, ela não muda:

P(A|B) = P(A).

Um exemplo

Seguimos com o exemplo de “gostar de chocolate” e “ter olho castanho”: qual a probabilidade de se ter olho castanho sabendo que alguém gosta de chocolate? Exatamente a mesma que seria caso ele não gostasse de chocolate. Uma simplesmente não afeta a outra.

Entendido isso, vamos utilizar a fórmula de Bayes apresentada anteriormente:

P(A|B) = P (A∩B) / P(B)

Passando P(B) para o outro lado multiplicando, obtemos:

P(A|B) * P(B) = P (A∩B)

Invertendo as posições, temos:

P (A∩B) = P(A|B) * P(B)

Ok, nós isolamos a intersecção, afinal, o que queremos saber é a intersecção de eventos independentes. Sabemos também, pelo explicado acima, que P(A|B) = P(A) em eventos independentes. Substituindo P(A|B) por P(A), obtemos:

P (A∩B) = P(A) * P(B)

Vemos que a intersecção de A com B, quando independentes, é a mera multiplicação de suas probabilidades individuais.

Como utilizar as dicas colocas nesse formulário

Pessoal, apresentamos diversos assuntos e fórmulas para serem Decoradas ou entendidas. Pode ser que pareça “fácil” decorá-las, afinal são apenas 4 fórmulas.

Acontece que essa é apenas uma parte de uma matéria dentro das diversas matérias de Estatística. Temos MUITAS fórmulas para decorar ao longo da matéria toda, reduzir esse número é primordial.

Ao contrário de Matemática Financeira, em que temos poucas fórmulas e muito raciocínio, estatística demanda a memorização de muitas fórmulas.

Dito isso, reforço que, quando possível, o aluno deve tentar entender a lógica de algo ao invés de decorá-la. Fica muito mais fácil memorizá-la uma vez que se sabe a lógica por trás dela do que a memorização “seca”.

Esperamos que essas dicas o ajudem a melhorar seu desempenho nas questões, já que muitos estudantes, por não lembrar do formulário, perdem uma questão que poderia, em outra situação, ser considerada razoavelmente simples.

Abraço

Julio Furlanetto

Assinatura Anual Ilimitada

Prepare-se com o melhor material e com quem mais aprova em Concursos Públicos em todo o país. Assine agora a nossa Assinatura Anual e tenha acesso ilimitado* a todos os nossos cursos.

ASSINE AGORA – Assinatura Ilimitada

Fique por dentro de todos os concursos:

Concursos abertos

Busque entender os Teoremas da Probabilidade mais a fundo: Para entender um pouco mais sobre Bayes, acesse https://pt.wikipedia.org/wiki/Teorema_de_Bayes