Resumo sobre Correlação Linear e Regressão para ISS-BH – Estatística
Olá, pessoal. Tudo certo? No artigo de hoje veremos o Resumo sobre Correlação Linear e Regressão para ISS-BH.
Os assuntos que serão vistos:
- Correlação Linear: Correlação de Pearson e Propriedades
- Regressão Linear Simples: Método dos Mínimos Quadrados e Coeficiente de Determinação
Sem mais delongas, vamos lá.
Correlação Linear
Vamos começar o Resumo sobre Correlação Linear e Regressão para ISS-BH.
Correlação: mostra a força que mantém duas variáveis unidas.
Correlação linear pode ser classificada:
- Direta (positiva): se aumentarmos uma variável, a outra também aumentará
- Inversa (negativa): se aumentarmos uma variável, a outra diminuirá
- Inexistente (nula): não existente correlação entre as variáveis
- Perfeita: os fenômenos se ajustam perfeitamente a uma reta
Vejamos graficamente.
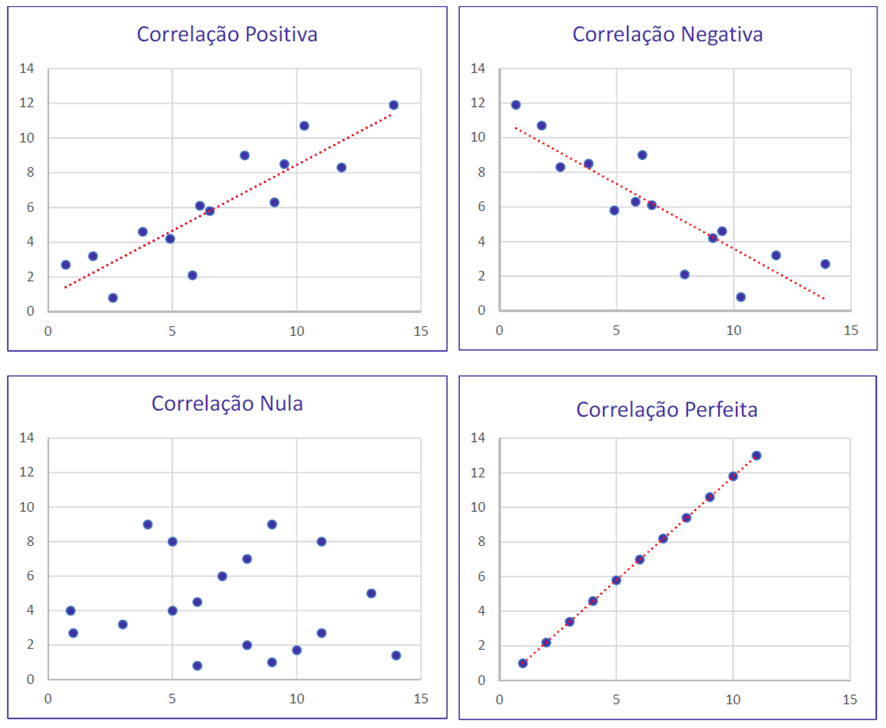
Coeficiente de correlação linear de Pearson
Dando continuidade, o coeficiente de correlação linear de Pearson mede o quão forte é a relação entre as duas variáveis (X e Y).
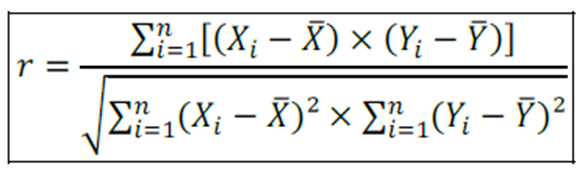
O somatório pode ser descrito alternativamente da seguinte forma:
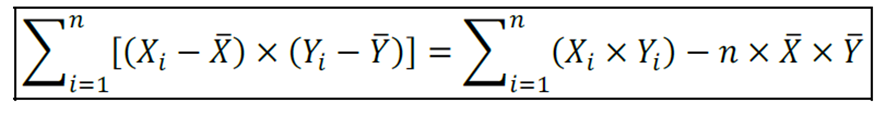
Para simplificar podemos descrevê-la simplesmente como:
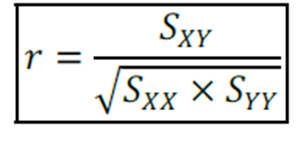
Também podemos encontrar o coeficiente de Pearson pela covariância entre as duas variáveis dividida pelo desvio padrão.
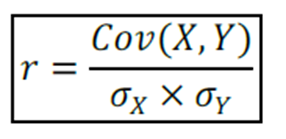
Ainda, é importante lembrar que o coeficiente de correlação de Pearson pode assumir quaisquer valores entre 1 e -1.
Obs.: Caso o coeficiente de Pearson for igual a zero, não podemos dizer necessariamente que não há relação, pois ela também poderá ser não-linear.
Vamos ver um exemplo numérico da utilização da fórmula.
Exemplo:
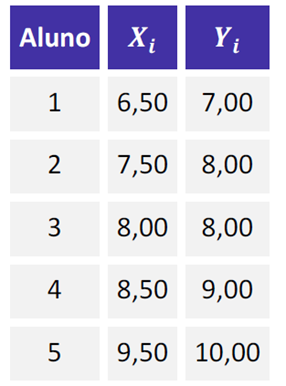
Teremos como média de X
= (6,50 + 7,50 + 8,00 + 8,50 + 9,50) / 5
= 8
E média de Y
(7,00 + 8,00 + 8,00 + 9,00 + 10,00) / 5
= 8,40
OK, agora veja os valores dos desvios do evento e a média, além dos demais valores que utilizaremos na fórmula.
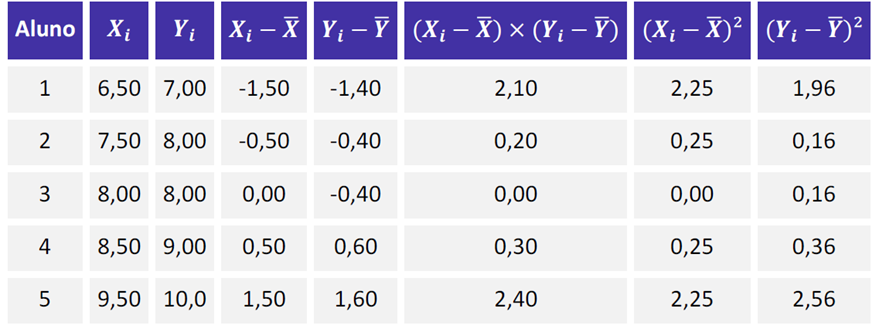
Assim, teremos que:

r = 5 / (5 x 5,2)^-2
r = 0,9805 (aproximadamente)
Propriedades do Coeficiente de Correlação
Agora vejamos duas importantes propriedades do Coeficiente de Correlação.
- 1ª Propriedade: não sofre alteração quando uma constante é adicionada /subtraída uma variável.
- 2ª Propriedade: não sofre alteração quando uma constante é multiplicada/dividida. Entretanto, constantes com sinais contrários, o coeficiente mudará de sinal.
Essa segunda propriedade pode ser um pouco mais difícil de entender, então vamos exemplificar. Para simplificarmos, saiba que o coeficiente de Pearson para os dados a seguir é igual a 1.
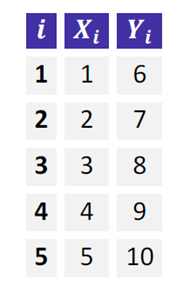
Agora vamos multiplicar os valores de X por -2 e Y por +2.
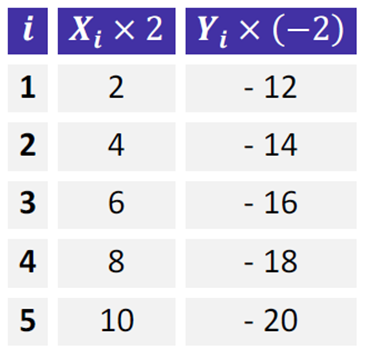
Teremos as seguintes médias
Média de X = (2+ 4 + 6 + 8 + 10) / 5
Média de X = 6
Média de Y = [(-12) + (-14) + (-16) + (-18) + (-20)] / 5
Média de Y = -16
Utilizando a tabela auxiliar de cálculo, assim como já fizemos teremos que:
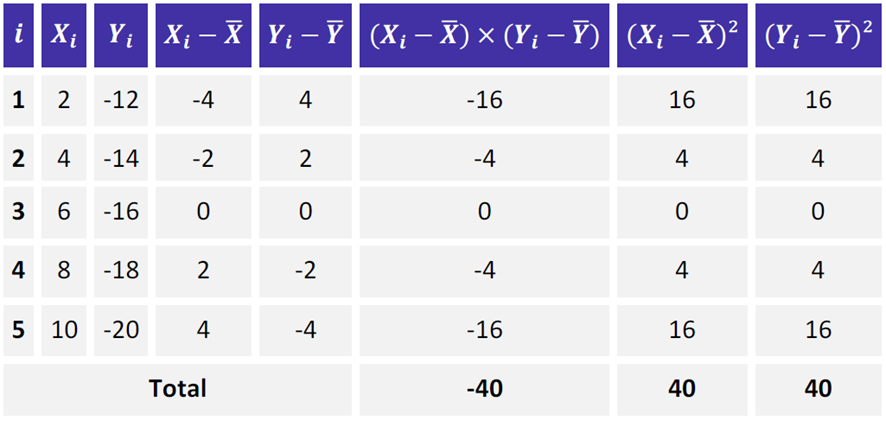
r = – 40 x (40 x 40)^-2
ou seja,
r (2x, -2Y) = -1
Veja que o valor do coeficiente não mudou, entretanto seu sinal foi alterado.
Regressão Linear Simples
Vamos dar continuidade ao Resumo sobre Correlação Linear e Regressão para ISS-BH, vendo agora a Regressão Linear Simples.
Basicamente a Regressão Linear Simples busca explicar a relação de uma variável (variável dependente – Y) com outra variável (variável independente – X).
Quanto a correlação, temos que:
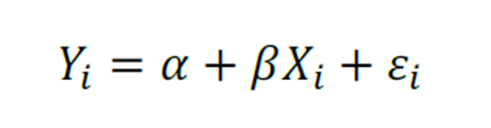
Yi = Variável dependente para uma série de observações
Xi = Variável independente para uma série de observações
β = coeficiente angular
α = coeficiente linear
ϵi = componente aleatório -> demonstra os desvios quando se tentar aproximar uma série de observações Xi por meio de uma reta Yi (correlação não perfeita)
Como qualquer modelo, a regressão linear exige alguns requisitos.
Requisitos:
- E (ϵi) = 0 -> média dos erros é igual a zero
- VAR (ϵi) = Constante -> A variância do erro é constante, trata-se da propriedade da homocedasticia.
- Cov (ϵi, ϵj ) = 0 -> os erros não são correlacionados, ou seja, são independentes.
Método dos Mínimos Quadrados
Continuando o Resumo sobre Correlação Linear e Regressão para ISS-BH, agora vejamos o Método dos Mínimos Quadrados.
Basicamente ele busca a reta que minimiza a soma dos quadrados dos desvios.
Utilizaremos a seguinte expressão:
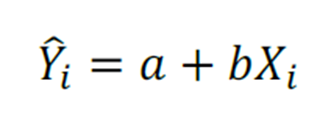
Em que “b” pode ser encontrado das seguintes formas
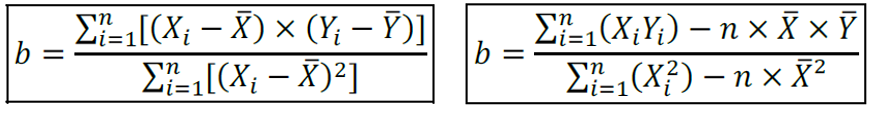
Ou de forma simplificada,
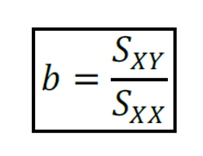
E “a”:
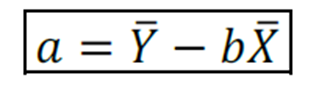
Para exemplificar, vamos utilizar a tabela auxiliar de cálculo.
Exemplo:
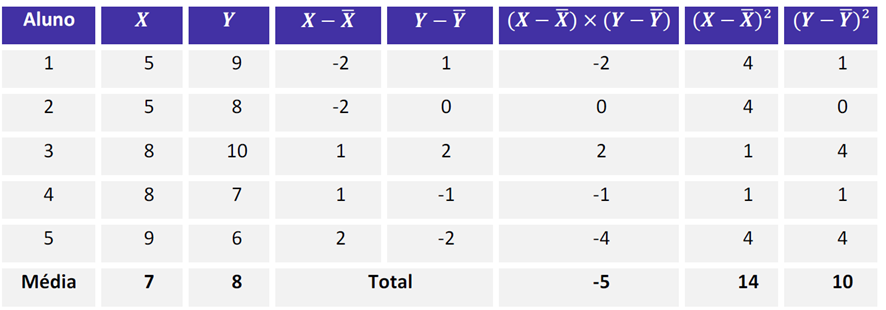
Teremos que,
b = -5 / 14
b = -0,357
E “a” será:
a = 8 – (-0,357) x 7
a = 8 + 2,499
a = 10,499
Logo, temos a reta de regressão estimada:
Y = 10,499 -0,357 . X
Coeficiente de Determinação
Para finalizar o Resumo sobre Correlação Linear e Regressão para ISS-BH.
O coeficiente de determinação (R²) mede a qualidade do ajuste proporcionado pela reta de regressão
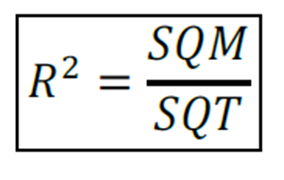
Perceba que se trata de um valor ao quadrado,
Sendo que:
SQT (Soma dos Quadrados Totais) = SQM (soma dos quadrados do modelo de regressão) + SQR (soma dos quadrados dos resíduos)
Em que a soma dos quadrados do modelo de regressão (SQM) pode ser definida pelas formas:
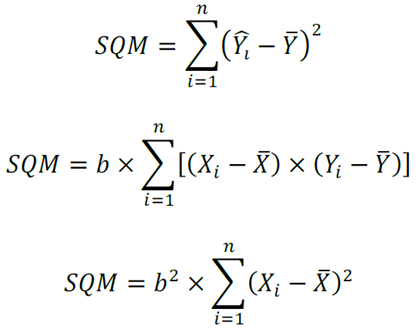
E a soma dos quadrados dos resíduos (SQR):
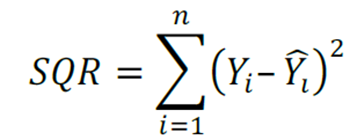
Exemplo: (VUNESP 2020/EBSERH) Numa regressão linear simples em que foi utilizada uma amostra com 52 observações, a soma dos quadrados totais e de 50 e a soma dos quadrados dos resíduos e de 20. O coeficiente de determinação será:
R² = SQM / SQT
R² = (SQT – SQR) / SQT
R² = (50 – 20) / 50
R² = 0,6
Considerações Finais
Pessoal, chegamos ao final dos Resumo sobre Correlação Linear e Regressão para ISS-BH. Espero que o artigo tenha sido útil para seu estudo.
Obviamente trata-se de um resumo apenas com as principais partes da matéria, as aulas são bem aprofundadas nas explicações e exercícios resolvidos, além de outros assuntos não tratados no artigo, mas que são importantes como Coeficiente de Determinação Ajustado, Quadrados Médios e Estatística F (Razão F), assim não deixe de acompanhar as aulas para o aprofundamento necessário.
Trata-se de um assunto que exige, de fato, muita prática por meio de exercícios. Assim, além dos exercícios da aula, não deixe de treinar pelo nosso sistema de questões.
Sistema de Questões (SQ) – Estratégia Concursos
Gostou do artigo? Não deixe de seguir
https://www.instagram.com/resumospassarin/
Cursos e Assinaturas
Prepare-se com o melhor material e com quem mais aprova em Concursos Públicos em todo o país.
Até mais e bons estudos!