Diagramas de Venn

Olá, pessoal! Como estão? Hoje, iremos tratar sobre os Diagramas de Venn. Esse tema, muitas vezes, não aparece expresso no edital, porém, usamos em diversas questões tanto de raciocínio lógico quanto de matemática em si. É um assunto básico, mas muito importante.

Conceito dos Diagramas de Venn

Incialmente, esse nome “Venn” se trata de homenagem ao matemático e filósofo britânico John Venn, que popularizou o método no século XIX para representar graficamente as relações lógicas entre conjuntos.

Nobres, um “conjunto” é a reunião de itens semelhantes, ou sejam que apresentam alguma particularidade em comum. Na matemática, simbologicamente, usamos chaves { } para representá-los.

Os Diagramas de Veen, nesse toada, trazem-nos uma apresentação mais visual das relações entre os conjuntos, de forma que saímos dessa “confusão” de letras e representações matemáticas e vamos para algo mais visual, que facilita nossa aprendizagem.

Assim, vamos supor que você está em sua sala de aula e separe seus colegas em dois grupos: quem pratica atletismo(A), quem joga basquete(B) e quem pratica ambos os esportes(atletismo e basquete).

Matematicamente, representaríamos essa expressão da seguinte forma:

(A U B) = (A) + (B) – (A ∩ B).

U significa União e ∩ significa interseção

Em que:

• (A U B) é quem pratica algum dos esportes ou ambos;
• (A) é quem pratica atletismo;
• (B) é quem pratica basquete;
• (A ∩ B) é quem pratica ambos os esporte.

Aplicação dos Diagramas de Venn

Vamos usar os Diagramas de Venn para representar nosso exemplo da sala de aula.

Vamos supor que 80(oitenta) pratiquem só atletismo; 100(cem) só basquete, 20(vinte) pratique ambos os esportes e 10(dez) não pratique nenhum dos esportes. Como ficaria o Diagrama de Venn?

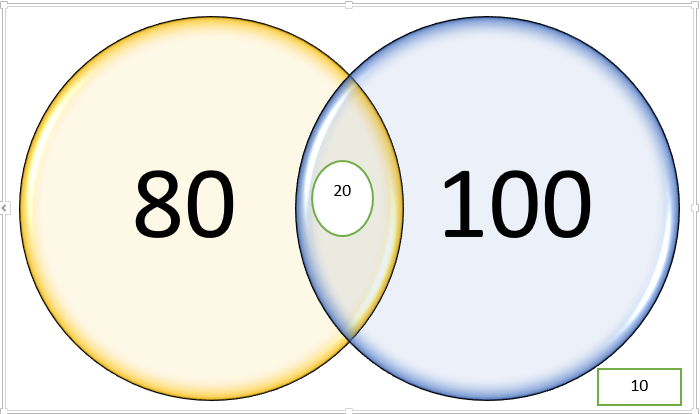
Entretanto, nobres, observem uma coisa: Há 20(vinte) alunos que participam dos dois grupos e, assim, se pedíssemos quantos alunos praticam algum esporte, o resultado não poderia ser alcançado somando 80+20+100+20 = 220, pois estaríamos “contando” o 20(vinte) duas vezes.

Voltemos à formula para entender:

(A U B) = (A) + (B) – (A ∩ B)

(A U B) = [80 + 20] + [100 + 20] – 20

Logo, (A U B) = 200

Ou seja, o nº de alunos que pratica “algum” esporte é 200(duzentos).

Logo, amigo(as), é isso que o diagrama faz, ele sistematiza, de maneira visual, a relação e os valores entre os grupos.

Então, nas questões, fiquem atentos. Se a banca citar: “100 alunos praticam atletismo”. Nesse valor está embutido tanto que pratica só atletismo, quanto quem pratica atletismo e outro esporte.

Apesar de o Diagrama de Venn com dois conjuntos ser bem conhecido, o que possui 3(três) conjuntos é o que mais cai em prova.

Vejamos a imagem:

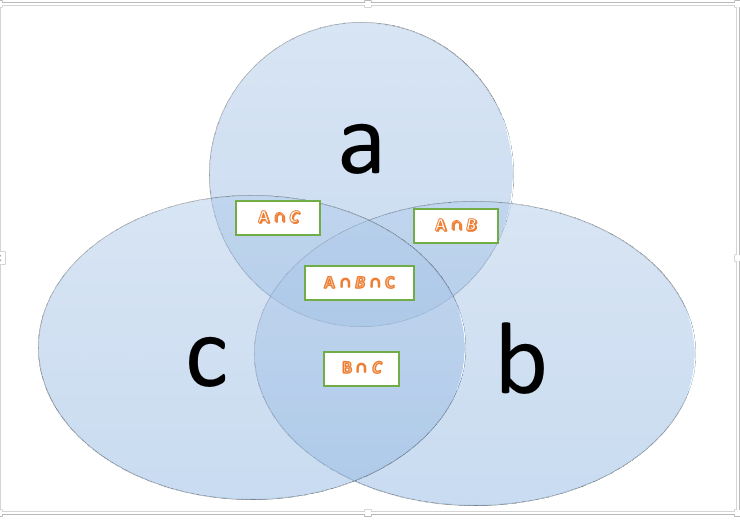
Observem que a lógica é a mesma (a, b e c) e suas interseções.

A fórmula matemática é:

n(A∪B∪C)=n(A)+n(B)+n(C)−n(A∩B)−n(A∩C)−n(B∩C)+n(A∩B∩C)

Exemplo dos Diagramas de Venn prática

Vamos usar uma questão recentíssima cobrada no concurso da Guarda Civil Municipal de Paulista (PE) aplicada pela IGEDUC.

Foi realizado um levantamento em uma turma de 60 alunos, sobre a frequências dos alunos em três disciplinas optativas: Matemática, Física e Química. Os resultados foram:

30 alunos frequentam as aulas de Matemática;

25 frequentam as aulas de Física;

20 frequentam as aulas de Química;

12 frequentam as aulas de Matemática e Física;

8 frequentam as aulas de Matemática e Química;

6 frequentam as aulas de Física e Química;

4 frequentam as aulas das três disciplinas.

Com base nestas informações, assinale a alternativa que apresenta corretamente quantos alunos não frequentam nenhuma das três disciplinas?

• (A) 7 alunos.
• (B) 5 alunos.
• (C) 9 alunos.
• (D) 11 alunos.

Comentários: Vamos montar o diagrama tal qual aprendemos – Obs. Na prova, pessoal, sugerimos que desenhem mesmo, ok?!

Dica 1: Nos Diagramas de Venn, sempre comecem pela interseção dos 3(três) conjuntos(interseção central). Nesse caso, 4 alunos frequentam as 3(três) disciplinas.

Após, de todas as demais interseções, diminuam o valor correspondente às 3(três) interseções a fim de não incorrer em dupla contagem. Vamos ver como fica nosso diagrama apenas com esses dados:

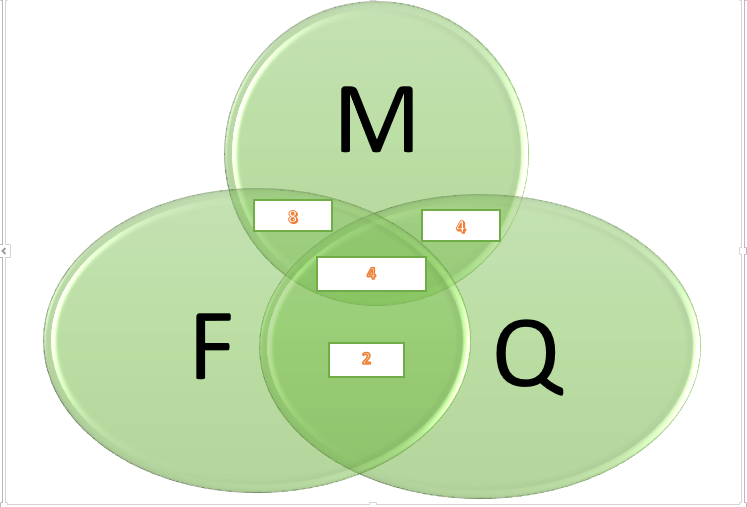
Visualizem que o valor das 3(três) interseções – valor central do gráfico – se manteve. Já das demais interseções, precisamos subtrair o valor da interseção central. Ficou assim:

• M∩F = 12(dado na questão) – 4(quem faz as 3 matérias) = 8
• M∩Q = 8(dado na questão) – 4(quem faz as 3 matérias) = 5
• F∩Q = 6(dado na questão) – 4(quem faz as 3 matérias) = 2

Dica 2. Só após achar as interseções, encontre quem pertence “exclusivamente” a um só conjunto.

Vamos matéria por matéria:

• Física: 25(dado na questão) – 8 – 4 – 2. Logo F = 11;
• Matemática: 30(dado na questão) – 8 – 4 – 4. logo M = 14;
• Química: 20(dado na questão) – 4 – 4 – 2. Logo Q = 10

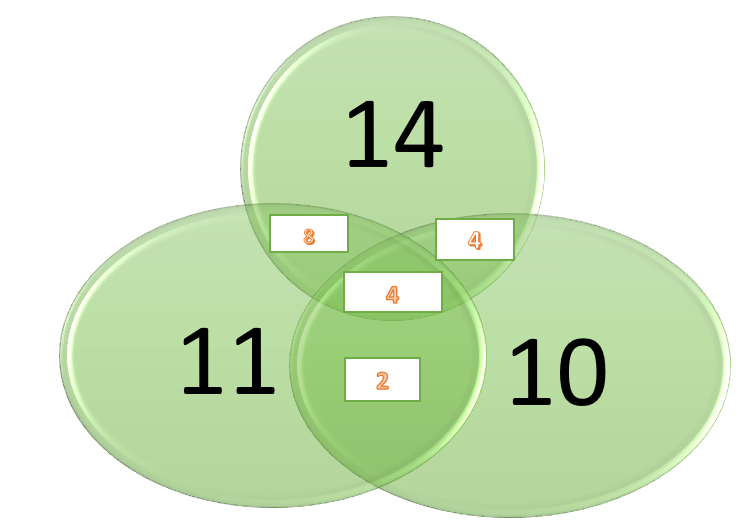
A questão solicita quantos dos 60(sessenta) alunos não frequentam nenhuma das 3 matérias.

Aí, é só somar todos os valores do Diagrama: 14 + 11 + 10 + 8 + 4 + 4 + 2 = 53.

Dessa forma, 60 – 53 = 7 alunos não frequentam nenhuma das matérias. Gab. A

Conclusão

Nobres, é isso que tínhamos para falar sobre os Diagramas de Venn. É uma ferramenta muito útil quando estamos diante de questões quem envolvem conjuntos. Reforçamos mais uma vez atenção na leitura da questão para a correta interpretação e inserção dos valores do diagrama. E, na hora da prova, tentem desenhar para evitar “perder” uma questão por “Bobeira”.

Abraços e bons estudos!

Quer estar antenado aos próximos concursos previstos? Confira nossos artigos!

Concursos Abertos

Concursos 2026