Resumo sobre raciocínio lógico matemático

Entenda sobre o raciocínio lógico matemático.

Olá pessoal, tudo bem?

Muitos concurseiros já perceberam que o conhecimento matemático adquirido no colégio já não é suficiente para responder muitas questões de concurso. Isso porque o que se exige do futuro ocupante de cargo público não é mais a sua simples capacidade de fazer cálculos ou decorar fórmulas, mas sim de raciocinar e resolver questões de forma lógica.

Em outras palavras, espera-se que o candidato associe Lógica e Matemática para resolver questões usando raciocínio eficiente e sistematizado. Se não ficou tão claro ainda, vamos iniciar um detalhamento sobre o raciocínio lógico matemático para esclarecer.

O que é o raciocínio lógico matemático?

O raciocínio lógico matemático pode ser entendido como a capacidade de analisar, resolver problemas, deduzir e identificar padrões utilizando princípios lógicos e matemáticos. É uma forma estruturada de pensar e obter resultado unindo Matemática e Lógica (que tem origem na Filosofia).

Formas de usar o raciocínio lógico matemático

Embora seja uma forma estruturada de raciocinar, não possui um padrão definido (por não se tratar unicamente de ciência exata). Apesar disso, podem ser usados esquemas e passo a passo para se obter o resultado pretendido.

Dessa maneira, podemos identificar algumas formas de se desenvolver o raciocínio lógico matemático mais comuns. Vejamos em seguida:

Teoria dos conjuntos

É uma das formas mais básicas de raciocínio lógico matemático. Envolve conhecimentos que abrangem noções de exclusão/inclusão de elementos ou operações com conjuntos.

Exemplo:
(CRM ES 2016 – Quadrix) Numa pesquisa, verificou-se que, das pessoas consultadas, 100 se informavam pelo site A; 150 por meio do site B; 20 buscavam se informar por meio dos dois sites, A e B; e 110 não se informavam por nenhum desses dois sites.
Desse modo, é correto afirmar que o número de pessoas consultadas nessa pesquisa foi de…

R = Observe que a questão não diz que as pessoas que se informavam pelo site A ou B utilizavam somente um desses sites. Logo, as 20 pessoas que utilizavam os dois sites também estão incluídas nas 100 que usavam o site A e nas 150 que usam o site B. Assim devemos descontar essas pessoas desses dois valores, ou seja, (100 – 20) + (150 – 20) + 20 + 110 = 340.

Lógica de argumentação

Baseada em premissas e conclusão. Se todo A é B e todo B é C, logo todo A é C (pode ser usada também noções de conjuntos), por exemplo.

Lógica sequencial

Utilizada para determinar o próximo elemento de uma sequência baseando-se nos anteriores. Podem ser usadas noções de PA, PG ou outra forma de identificação de padrões.

Raciocínio geométrico-espacial

Baseada em análise de figuras que podem envolver rotações, dobraduras, planificações, contagem de seus elementos e etc.

Lógica proposicional

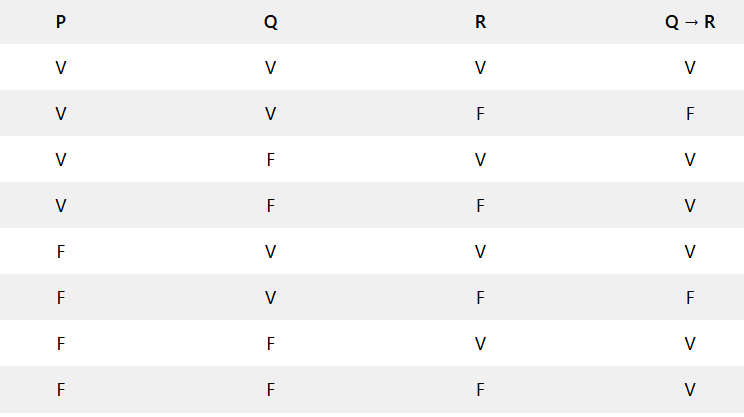
É uma das mais estruturadas do raciocínio lógico matemático, por apresentar representação e conceitos padronizados. Assim, utiliza conectivos, tabelas verdades e equivalências lógicas para se obter o resultado.

Para alcançar o resultado de uma análise, são utilizadas proposições (afirmações que podem ter apenas dois valores: verdadeiro ou falso). Essas proposições são relacionadas entre si por meio de conectivos (E, OU, SE…ENTÃO, SE E SOMENTE SE, NÃO), que irão definir o resultado da sentença.

Por exemplo: utilizando a sentença “vou estudar E dormir cedo”. Temos duas proposições: “vou estudar” e “(vou) dormir cedo”. Elas estão conectadas pelo conectivo E.

Desse modo, a sentença completa só pode ser verdadeira se cumpridas as duas afirmações. Ou seja, caso alguém afirme que vai fazer uma coisa E outra, o conjunto das afirmações só pode ser verdade se ambas forem.

Outros raciocínios

O raciocínio lógico matemático não se restringe a casos específicos. Não é incomum localizar em concursos questões que envolvam casos como:

• Dois personagens em que um sempre mente e outro sempre fala a verdade;
• Personagens que fazem afirmações excludentes (identificada a característica de um personagem, nenhum outro pode possuí-la);
• Repartição de bens seguindo uma lógica específica.
• Relação matemática entre características de personagens (idade, altura, peso, posse, velocidade, etc.).

Como resolver questões de raciocínio lógico matemático

Primeiramente, o fator mais importante de qualquer resolução é a interpretação da questão. Leia com muita atenção o enunciado, pois isso é essencial para saber de onde partir e para onde ir.

Em seguida, siga as seguintes etapas:

• Atenha-se ao contexto da questão e não se prenda a visões pessoais ou sociais. Algumas questões costumam vir com construções sem fundamento no senso comum, como “todo gato é um inseto”. Você deve aceitar a afirmação como possível verdade a não ser que a questão permita que você deduza.
• Verifique se o problema já possui alguma resolução padrão, como na lógica proposicional e questões que envolvem conjuntos;
• Se sim, transfira as informações para a linguagem lógica/matemática e não fuja das regras específicas. Na lógica proposicional, por exemplo, toda vez que o conectivo OU é usado, a sentença só vai ser falsa se ambas as afirmações forem falsas. Não fuja disso e não questione.
• Se não, organize os dados visualmente, crie relação entre eles e elimine as possibilidades impossíveis. Por exemplo, se a questão fala de personagens em fila, desenhe os espaços na fila e vá encaixando os elementos segundo as dicas da questão.
• Sempre que possível, divida o problema em partes ou etapas de análise.
• Se não conseguir completar o raciocínio seguinte somente as dicas da questão, vá até onde conseguir acompanhar e teste algumas possibilidades a partir daí.
• Obtendo uma reposta, teste se ela é plausível ou se responde ao questionamento do enunciado.

Considerações finais

O raciocínio lógico matemático está cada vez mais presente nas provas de concursos e busca estimular o candidato a uma forma de pensar além da matemática. Isso traz resultados benéficos inclusive para a forma de pensar no dia a dia.

Utilizar o raciocínio lógico matemático em questões de concursos demanda prática e dedicação aos estudos. Mas o resultado sempre vem quando o esforço supera desânimo.

Bons estudos!!!

Quer saber quais serão os próximos concursos? 

Confira nossos artigos! 

Concursos abertos 

Concursos 2026