Inequações do 2º Grau

Aprenda os conceitos essenciais sobre inequações do 2º grau com um resumo para as principais provas de concursos.

Olá, pessoal! Tudo bem com vocês?

As inequações do 2º grau são uma extensão das equações do 2º grau e aparecem com muita frequência em concursos como FGV, Cebraspe, FCC e Quadrix.
Ao contrário das equações, que buscam os valores exatos de x, as inequações procuram intervalos em que a expressão quadrática é positiva, negativa, não positiva ou não negativa.

Neste artigo, vamos entender como funcionam as inequações do 2º grau, com explicações e exemplos que facilitam a compreensão, para que você possa revisar a matéria de forma rápida e estratégica.

Confira os tópicos que serão abordados:

• O que são inequações do 2º grau;
• Tipos de inequações do 2º grau;
• Como resolver inequações do 2º grau;
• Exercício resolvido;
• Resumo.

O Que São Inequações do 2º Grau

As inequações são semelhantes às equações, mas em vez de igualdade (=), apresentam desigualdade entre as expressões. Ou seja, mostram quando uma expressão é maior, menor, maior ou igual, ou menor ou igual que outra.

Uma inequação do 2º grau é uma desigualdade envolvendo uma expressão quadrática, que possui um dos seguintes formatos:

• ax² + bx + c > 0
• ax² + bx + c ≥ 0
• ax² + bx + c < 0
• ax² + bx + c ≤ 0

Os símbolos usados são:

Símbolo	Leitura
>	maior que
<	menor que
≥	maior ou igual a
≤	menor ou igual a

Exemplos de inequações do 2º grau:

• x² – 4x + 3 > 0
• 2x² + 5x ≥ 3
• -x² + 9 < 0

Assim como nas equações de 2º grau, devemos encontrar a forma reduzida:

ax² + bx + c

Tipos de Inequações do 2º Grau

As inequações podem ser classificadas de acordo com o sinal do coeficiente a:

Tipo	Sinal de “a”	Forma da parábola	Tendência
Concavidade para cima	(a > 0)	U	A expressão tende a +∞
Concavidade para baixo	(a < 0)	∩	A expressão tende a −∞

Além disso, a natureza das raízes da equação associada ax² + bx + c = 0 determina a resposta.

Discriminante (Δ)	Raízes	Efeito na inequação
Δ > 0	2 raízes reais distintas	A parábola cruza o eixo x → muda de sinal
Δ = 0	1 raiz real (dupla)	A parábola toca o eixo x → o sinal só muda no ponto
Δ < 0	Sem raízes reais	A parábola não cruza o eixo x → sinal é constante

Essas informações são essenciais para o estudo do sinal, principal método utilizado.

Como Resolver Inequações do 2º Grau

O método mais usado para resolver inequações do 2º grau em provas é o estudo do sinal da função quadrática.

1º Passo) Transformar a inequação em equação e encontre as raízes

Resolva:

ax² + bx + c = 0

para encontrar as raízes.

2º Passo) Identificar a concavidade

• Se a > 0, concavidade para cima – U – positiva fora das raízes;
• Se a < 0, concavidade para baixo –∩ – positiva entre as raízes.

3º Passo) Construir a reta de sinais (estudo do sinal)

Coloque as raízes encontradas na reta numérica e analise os intervalos.

4º Passo) Escolher os intervalos desejados

De acordo com a desigualdade:

• Maior que zero (> 0) → escolher regiões positivas.
• Menor que zero (< 0) → escolher regiões negativas.
• Com igualdade (≥ ou ≤) → incluir as raízes.

Exercício Resolvido

(VUNESP – Prefeitura de Rio Claro – Professor de Educação Básica II – 2022) A solução da inequação do 2º grau –x² – 3x ≤ –10 é corretamente apresentada na alternativa:

a) [–∞, –5] ∪ [2, +∞]
b) [–∞, –2] ∪ [5, +∞]
c) [–5, 2]
d) [–2, 5]
e) [–3, 10]

1) Encontrando as raízes da equação associada:

–x² – 3x ≤ –10
–x² – 3x + 10 ≤ 0
-x² – 3x + 10 = 0 → a = -1; b = -3; c = 10

Utilizando a fórmula de Bhaskara, chegamos em:

Δ = (-3)² – 4.(-1).10 = 49

2) Identificando a concavidade:

Como a = -1 < 0, a parábola possui concavidade para baixo (∩).

3) Estudo do sinal:

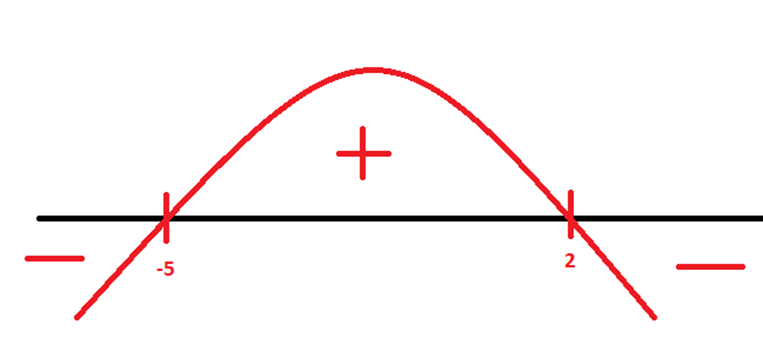
4) Escolha do intervalo:

Como queremos a parte negativa do intervalo (–x² – 3x + 10 ≤ 0), devemos escolher os valores menores que -5 e os maiores que 2. Além disso, como a desigualdade é menor ou igual (≤), também devemos incluir as raízes -5 e 2.

Portanto, a resposta correta é a alternativa “a”: [–∞, –5] ∪ [2, +∞].

Finalizando – Inequações do 2º Grau

As inequações do 2º grau aparecem frequentemente em provas de concursos, e dominar o estudo do sinal é essencial para resolvê-las com rapidez e segurança. O método é simples: basta encontrar as raízes, analisar a concavidade e identificar os intervalos adequados. A chave para o domínio está na prática.

É importante reforçar que este conteúdo deve ser utilizado como complemento ao material em PDF, onde a abordagem é aprofundada e completa. Além disso, é fundamental praticar com muitas questões, preferencialmente separadas por banca, para entender as diferentes formas de cobrança.

Quer se aprofundar no tema? O Estratégia Concursos disponibiliza materiais em PDF completos e atualizados, com teoria detalhada, questões comentadas e videoaulas direcionadas para cada concurso. Com prática e um bom material, você estará preparado para resolver qualquer questão de inequações do 2º grau que aparecer na sua prova.

Acesse os cursos do Estratégia Concursos e fortaleça sua preparação com um conteúdo de alto nível.

Bons estudos e até a próxima!

Cursos e Assinaturas

Prepare-se com o melhor material e com quem mais aprova em Concursos Públicos em todo o país!

Concursos Abertos

Concursos 2025