Equações do 2º Grau

Aprenda os conceitos essenciais sobre equações do 2º grau com um resumo para as principais provas de concursos. 

Olá, pessoal! Tudo bem com vocês? 

Quando se trata de Matemática e Raciocínio Lógico, alguns temas são recorrentes nos mais variados tipos de concurso. É o caso das equações do 2º grau, um dos pilares da matemática, que aparecem com frequência em questões de concursos públicos, tanto de nível médio quanto superior, em editais de bancas como FGV, Cebraspe e FCC. 

As equações do 2º grau estão presentes em problemas de raciocínio lógico, geometria, juros compostos e funções quadráticas, e exigem do candidato a capacidade de identificar o tipo de equação, escolher o método correto de resolução e interpretar o resultado. 

Neste artigo, vamos estudar os principais pontos sobre as equações do 2º grau, com exemplos, para que você possa revisar a matéria de forma rápida e estratégica. 

Confira os tópicos que serão abordados: 

• O que são equações do 2º grau; 
• Tipos de equações do 2º grau (completas e incompletas); 
• Como resolvê-las; 
• Exemplo resolvido; 
• Resumo final para fixar o conteúdo. 

O Que São Equações do 2º Grau? 

Uma equação do 2º grau, ou equação quadrática, é toda equação que pode ser escrita na forma: 

ax² + bx + c = 0 

em que: 

• a, b e c são números reais, chamados de coeficientes; 
• a ≠ 0 (pois, se fosse 0, ela se tornaria uma equação do 1º grau); e 
• x é a incógnita. 

Essa é a forma reduzida da equação quadrática, sendo que o termo “ax²” é o termo quadrático, “bx” é o linear, e “c” é o constante (pois não depende do valor de x). 

Por exemplo: 2x² + 3x – 5 = 0 

Aqui, temos: a = 2, b = 3, c = –5 

Caso a equação esteja em outro formato, devemos transformá-la na forma reduzida, como no exemplo abaixo: 

x² + 2x = 2x² – 5x + 2 
x² + 2x – 2x² + 5x – 2 = 0 
-x² + 7x – 2 = 0 → a = -1, b = 7, c = -2 

Tipos de Equações do 2º Grau 

As equações do 2º grau podem ser classificadas em completas e incompletas. 

Tipo	Forma geral	Características	Exemplo
Completa	ax² + bx + c = 0	Possui os três coeficientes (a, b e c) diferentes de zero	2x² + 3x – 5 = 0
Incompleta (b = 0)	ax² + c = 0	Não possui o termo linear (b = 0)	x² – 9 = 0
Incompleta (c = 0)	ax² + bx = 0	Não possui o termo constante (c = 0)	x² – 2x = 0
Incompleta (b = 0 e c = 0)	ax² = 0	Possui apenas o termo quadrático	5x² = 0

Como Resolver Equações do 2º Grau 

Equações Incompletas 

Quando b = 0 ou c = 0, as equações do 2º grau podem ser resolvidas sem precisar da fórmula de Bhaskara. 

1º Caso) b = 0 → ax² + c = 0 

ax² = -c 

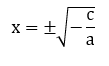
Exemplo: 

x² – 9 = 0 
x² = 9 
x = ±3 

As soluções são x = 3 e x = -3. 

2º Caso) c = 0 → ax² + bx = 0 

Nesse caso, fatoramos a incógnita comum: 

x(ax + b) = 0 

Portanto: 

x = 0    ou    ax + b = 0 → x = -b/a 

Exemplo: 

x² – 5x = 0 
x(x – 5) = 0 
x = 0 ou x = 5 

3º Caso) Apenas ax² = 0 

Se só o termo quadrático existe: 

ax² = 0 → x = 0 

Equações Completas 

Para as equações completas do 2º grau, utiliza-se a fórmula de Bhaskara, que deriva da aplicação da fórmula resolutiva: 

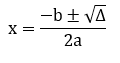
A expressão dentro da raiz é chamada de delta ou discriminante (Δ): 

Δ = b² – 4ac 

O valor do discriminante define a quantidade de raízes reais da equação de 2º grau: 

Valor de Δ	Natureza das raízes	Exemplo
Δ > 0	Duas raízes reais e distintas	x² – 5x + 6 = 0 → x’ = 2 e x” = 3
Δ = 0	Duas raízes reais e iguais	x² – 4x + 4 = 0 → x’ = x” = 2
Δ < 0	Nenhuma raiz real (raízes complexas)	x² + 4x + 8 = 0

Exemplo Prático Resolvido 

Um pintor está pintando um quadro retangular, de tal forma que o comprimento deve ser dois metros maior do que a largura, e a área total deve ser de 8 m². Sendo x a medida do comprimento do quadro, em metros, encontre suas dimensões. 

Chamando a largura do retângulo de x, seu comprimento deverá ser x + 2. 

A área de um retângulo é determinada pelo produto entre a base e a altura, e, nesse caso, é igual a 8. Portanto: 

A = x(x + 2)
x(x + 2) = 8 
x² + 2x – 8 = 0 → a = 1, b = 2, c = -8 

O discriminante da equação será: 

Δ = b² – 4ac
Δ = 2² – 4.1.(-8)
Δ = 36 

Finalmente, utilizando a fórmula de Bhaskara: 

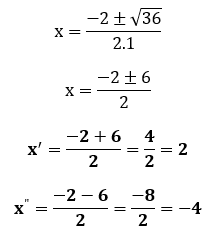
Resumo 

Para te ajudar a revisar tudo o que vimos até aqui de forma estratégica, preparamos uma tabela com as principais características de cada tipo de equações do 2º grau: 

Tipo de equação	Forma	Método de resolução	Fórmula	Exemplo	Soluções
Completa	ax² + bx + c = 0	Fórmula de Bhaskara		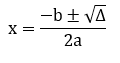2x² – 3x – 5 = 0	2,5 e -1
Incompleta (b = 0)	ax² + c = 0	Isolamento de x	x = ±√(-c/a)	x² – 9 = 0	3 e -3
Incompleta (c = 0)	ax² + bx = 0	Fatoração	x = 0 ou x = -b/a	x² – 2x = 0	0 e 2
Incompleta (só ax²)	ax² = 0	Divisão direta	x = 0	5x² = 0	0

Finalizando – Equações do 2º Grau 

Dominar as equações do 2º grau é essencial para quem presta concursos públicos, pois elas aparecem tanto em questões diretas de matemática quanto em problemas contextualizados, como os que envolvem área, movimento uniformemente variado, juros compostos ou funções quadráticas. A chave para o domínio está na prática. 

Saber identificar o tipo de equação, aplicar o método adequado e interpretar o discriminante faz toda a diferença na hora da prova — e pode garantir pontos valiosos em disciplinas de raciocínio lógico e matemática básica. 

É importante reforçar que este conteúdo deve ser utilizado como complemento ao material em PDF, onde a abordagem é aprofundada e completa. Além disso, é fundamental praticar com muitas questões, preferencialmente separadas por banca, para entender as diferentes formas de cobrança. 

Quer se aprofundar no tema? O Estratégia Concursos disponibiliza materiais em PDF completos e atualizados, com teoria detalhada, questões comentadas e videoaulas direcionadas para cada concurso. Com prática e um bom material, você estará preparado para resolver qualquer questão de operadores lógicos que aparecer na sua prova. 

Acesse os cursos do Estratégia Concursos e fortaleça sua preparação com um conteúdo de alto nível. 

Bons estudos e até a próxima! 

Cursos e Assinaturas

Prepare-se com o melhor material e com quem mais aprova em Concursos Públicos em todo o país!

Concursos Abertos

Concursos 2025