Probabilidade Condicional e Teorema de Bayes
Aprenda os conceitos essenciais sobre probabilidade condicional e Teorema de Bayes com um resumo para as principais provas de concursos.
Olá, pessoal! Tudo bem com vocês?
A probabilidade condicional e o Teorema de Bayes formam um dos núcleos mais importantes da probabilidade aplicada em concursos públicos. Esses temas aparecem com frequência em questões de bancas como FGV, CEBRASPE e FCC, que envolvem testes, diagnósticos, urnas, cartas, pessoas selecionadas e situações em que um evento altera a chance de ocorrência de outro.
Neste artigo, vamos estudar a probabilidade condicional e o Teorema de Bayes, suas propriedades e aplicá-los em exemplos, para que você possa revisar a matéria de forma rápida e estratégica.
Confira os tópicos que serão abordados:
- O conceito básico de probabilidade;
- O que é probabilidade condicional;
- O Teorema de Bayes e sua interpretação;
- Dois exemplos resolvidos;
- Um resumo final para revisão rápida.
O Que é Probabilidade?
A probabilidade mede o grau de chance de ocorrência de um evento aleatório.
Ela é definida pela razão entre o número de casos favoráveis e o número de casos possíveis (total de casos), desde que todos tenham a mesma chance de ocorrência.
Exemplo:
Ao lançar um dado honesto, a probabilidade de sair o número 4 é:
Algumas propriedades importantes:
- 0 ≤ P(A) ≤ 1: a probabilidade de um evento está sempre entre 0 e 100%;
- P(A) = 0: evento impossível (0%);
- P(A) = 1: evento certo (100%);
- A soma das probabilidades de todos os resultados possíveis é igual a 1 (100%).
Probabilidade Condicional
A probabilidade condicional é a probabilidade de um evento ocorrer sabendo que outro evento já ocorreu.
Ela é indicada por: P(A|B)
Lê-se: probabilidade de A, dado que B ocorreu.
Fórmula da probabilidade condicional
Para calcular a probabilidade condicional, utiliza-se a seguinte fórmula:
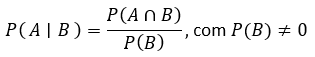
Onde:
P(A∩B): probabilidade da interseção de A com B, ou seja, probabilidade de A e B ocorrerem simultaneamente;
P(B): probabilidade de B.
Ou seja, o espaço amostral é reduzido, pois a condição imposta pelo evento B altera o conjunto de possibilidades.
Probabilidade condicional e eventos independentes
Dois eventos A e B são independentes quando a ocorrência de um não altera a probabilidade de ocorrência do outro. Em termos práticos, isso significa que o conhecimento prévio de um evento não fornece informação adicional sobre o outro.
Do ponto de vista matemático, a independência pode ser caracterizada pela seguinte igualdade:
P(A|B) = P(A)
De forma equivalente, a independência também pode ser expressa por:
P(A∩B) = P(A) . P(B)
Em concursos públicos, situações de eventos independentes aparecem com frequência em experimentos repetidos ou simultâneos, como lançamentos sucessivos de moedas ou dados, bem como em retiradas com reposição, nas quais o espaço amostral permanece o mesmo após cada experimento.
Por exemplo:
Ao lançar uma moeda duas vezes, o evento “sair cara no primeiro lançamento” é independente do evento “sair cara no segundo lançamento”. Assim, a probabilidade de ocorrerem duas caras é:
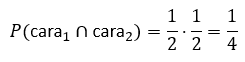
Além disso, é importante destacar que a independência não pode ser presumida sem análise do enunciado. Sempre que a ocorrência de um evento modificar o espaço amostral ou as probabilidades envolvidas, os eventos serão dependentes, e a probabilidade condicional deverá ser aplicada de forma adequada.
Exemplo
Em um baralho, sabendo que a carta retirada é vermelha, qual a probabilidade de ela ser de copas?
- Cartas vermelhas: 26
- Copas: 13
- Total de cartas: 52
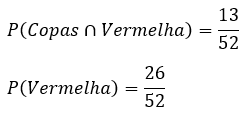
Portanto:
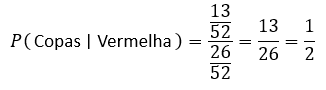
O Teorema de Bayes na Probabilidade Condicional
O Teorema de Bayes permite inverter uma probabilidade condicional, isto é, calcular P(A|B) a partir de P(B|A).
Ele é muito explorado em provas por exigir atenção ao enunciado e organização das informações.
Fórmula do Teorema de Bayes
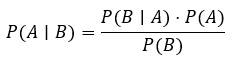
Exemplos Resolvidos – Probabilidade Condicional e Teorema de Bayes
1) Probabilidade Condicional
Uma urna contém 3 bolas brancas e 2 bolas pretas. Retiram-se duas sem reposição.
Qual a probabilidade de a segunda bola ser branca, sabendo que a primeira foi branca?
Resolução:
Após retirar uma bola branca:
- Restam 2 bolas brancas
- Total de bolas restantes: 4
Portanto:
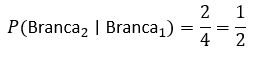
2) Teorema de Bayes
Em um baralho padrão de 52 cartas, sabe-se que uma carta é de ouros.
Qual é a probabilidade de essa carta ser um ás?
Definição dos eventos
- A: a carta é um ás
- B: a carta é ouros
Queremos calcular: P(A|B)
Dados:
- P(A): existem 4 ases em 52 cartas
- P(B): existem 13 cartas de ouros em 52
- P(B|A):dado que a carta é um ás, a chance de ela ser ouros é
Aplicação do Teorema de Bayes
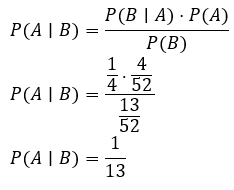
Observação: Quando há apenas uma causa, como nesse exemplo, é possível resolver também por razão direta, mas a banca costuma exigir a fórmula explícita.
Resumo Comparativo – Probabilidade Condicional e Teorema de Bayes
Para te ajudar a revisar tudo o que vimos até aqui de forma estratégica, preparamos uma tabela com os principais conceitos sobre probabilidade condicional e Teorema de Bayes:
| Conceito | Expressão | Observação |
| Probabilidade simples | P(A) | Mede a chance de um evento |
| Probabilidade condicional | P(A|B) | Evento A condicionado a B |
| Fórmula condicional | 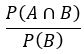 | Reduz o espaço amostral |
| Independência | P(A∩B) = P(A) . P(B) | Evento A não inefere no B |
| Teorema de Bayes | 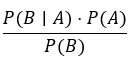 | Inverte a condição |
Finalizando – Probabilidade Condicional e Teorema de Bayes
A probabilidade condicional e o Teorema de Bayes são temas centrais em provas de concursos públicos, pois avaliam não apenas cálculo, mas principalmente interpretação lógica e organização das informações. Compreender a ideia de condicionar o espaço amostral e saber aplicar corretamente a fórmula de Bayes faz toda a diferença para evitar erros comuns. A chave para o domínio está na prática.
É importante reforçar que este conteúdo deve ser utilizado como complemento ao material em PDF, onde a abordagem é aprofundada e completa. Além disso, é fundamental praticar com muitas questões, preferencialmente separadas por banca, para entender as diferentes formas de cobrança.
Quer se aprofundar no tema? O Estratégia Concursos disponibiliza materiais em PDF completos e atualizados, com teoria detalhada, questões comentadas e videoaulas direcionadas para cada concurso. Com prática e um bom material, você estará preparado para resolver qualquer questão de probabilidade condicional e Teorema de Bayes que aparecer na sua prova.
Acesse os cursos do Estratégia Concursos e fortaleça sua preparação com um conteúdo de alto nível.
Bons estudos e até a próxima!
Cursos e Assinaturas
Prepare-se com o melhor material e com quem mais aprova em Concursos Públicos em todo o país!