Regra de três simples e composta – conceito e aplicação
O artigo de hoje é dedicado aos estudantes que têm dificuldades com matemática, em especial, com a regra de três simples e composta.
Abordaremos o tema de forma bem prática para facilitar seu aprendizado e garantir os pontos tão preciosos na hora da prova. Vamos lá?
O que é uma regra de três?
Regra de três é um método matemático que possibilita encontrar um valor até então desconhecido, considerando a proporcionalidade entre as variáveis já conhecidas. Essas variáveis podem ser diversas, tais como área, tempo, dinheiro etc.
Trata-se de um método muito útil para aplicações no dia a dia e o mais importante para nós: é muito cobrado em prova, direta ou indiretamente.
A relação das grandezas
Uma análise sempre necessária antes de “sair calculando” a regra de três é verificar se as variáveis são diretamente proporcionais ou se são inversamente proporcionais.
Dizemos que as variáveis são diretamente proporcionais quando o aumento de uma variável ocasiona o aumento da outra, ao passo que as variáveis são inversamente proporcionais quando o aumento de uma faz com que a outra diminua.
Exemplificando:
A velocidade média e o tempo de chegada no destino são variáveis inversamente proporcionais, afinal quanto maior a velocidade, mais rápido se chega (menos tempo).
Já a distância e o tempo (considerando uma velocidade média constante) são variáveis diretamente proporcionais, uma vez que quanto mais longe for (mais distante), maior será o tempo para se chegar ao destino.
Tranquilo, né?
Regra de três simples
Na regra de três simples temos duas variáveis e conhecemos três valores e desejamos encontrar o quarto. Vamos exemplificar.
Suponha que se estime 10 salgadinhos por pessoa para realizar uma festa de aniversário. Quantos salgadinhos precisarão ser adquiridos, caso se deseje convidar 20 pessoas?
Lembre-se que a primeira análise a ser realizada é a da proporcionalidade. Nesse caso, trata-se de duas variáveis diretamente proporcionais, uma vez que ao aumentar o número de convidados, deve-se comprar mais salgadinhos.
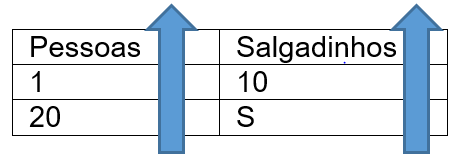
Assim,
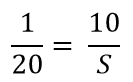
Multiplicando em “X”, teremos que:
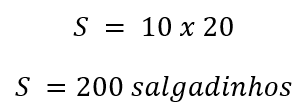
Agora vamos considerar outra situação.
Para construir uma casa, um pedreiro leva 30 dias. Quantos dias serão necessários para construir a casa se 5 pedreiros trabalharem simultaneamente?
As variáveis são inversamente proporcionais, afinal, quanto mais pedreiros trabalhando, menos dias serão necessários para concluir a obra.
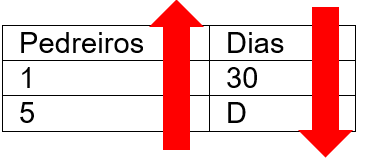
A consequência disso é que devemos “inverter” um dos lados da nossa igualdade, logo:
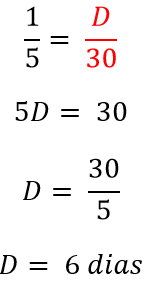
Regra de três composta
A regra de três composta é muito parecida com o que fizemos até aqui, porém, teremos três variáveis (às vezes até 4 em alguns exercícios) e 6 valores (ou 8, no caso de 4 variáveis), sendo um deles desconhecido.
Vamos pegar o exemplo anterior (da construção da casa) e acrescer um elemento: as horas trabalhadas por dia.
Imagine que para construir uma casa, um pedreiro leve 30 dias trabalhando 15 horas diárias. Quantos dias serão necessários para construir essa casa se 5 pedreiros trabalharem simultaneamente durante 10 horas diárias?
O primeiro passo para esse tipo de exercício é “determinar uma seta” e analisar quais serão as consequências para as demais variáveis.
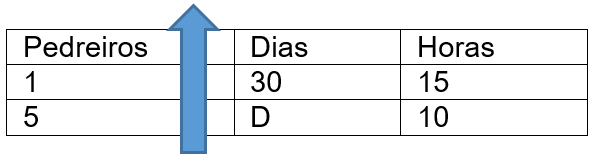
Analisando a proporcionalidade: Se a quantidade de pedreiros aumenta (seta para cima), a quantidade de dias para concluir a obra será menor (seta para baixo), da mesma forma que a quantidade de horas poderá ser menor (seta para baixo).
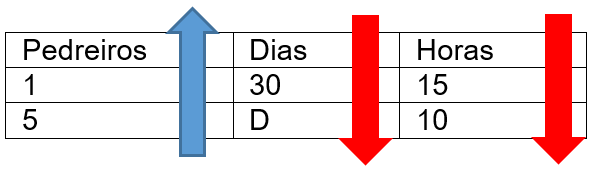
Em termos matemáticos, temos que:
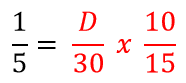
Percebeu? Houve a inversão das duas frações relacionadas aos dias e às horas, afinal, elas são inversamente proporcionais à quantidade de pedreiros.
Então,
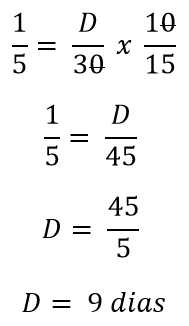
Vendo na prática
Caso ainda tenha restado alguma dúvida, nada melhor do que realizar algumas questões de concurso para sanar essas lacunas.
Iniciaremos com dois exemplos de regra de três simples.
Exemplos de regra de três simples
FCC – Auxiliar Legislativo/2020
Uma empresa de 60 funcionários deve entregar uma encomenda em 30 dias. Após 15 dias, apenas 3/10 da encomenda havia sido produzida. Considerando que o ritmo de produção de cada funcionário é igual e constante, o número adicional de funcionários que a empresa deve contratar para entregar a encomenda no prazo é
a) 100
b) 20
c) 40
d) 60
e) 80
Vamos iniciar com a tabela das variáveis, considerando que o “o ritmo de produção de cada funcionário é igual e constante” e que o prazo para finalizar a encomenda é de 15 dias (30 dias totais, menos 15 dias que já foram gastos para produzir 3/10).

A variável “Dias” é a mesma, então, podemos desconsiderá-la, pois seria uma fração 15/15, logo:
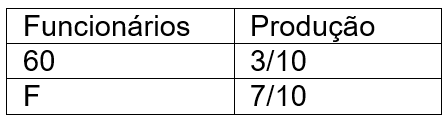
Analisando a proporcionalidade: Quanto mais funcionários, mais se produz, então:
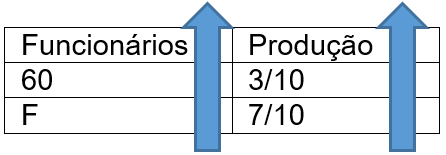
Assim,
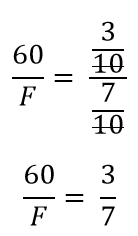
Multiplicando em “X”:
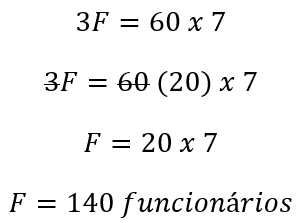
Lembrando que queremos o “número adicional de funcionários que a empresa deve contratar”, então teremos que subtrair do total de funcionários os já existentes.
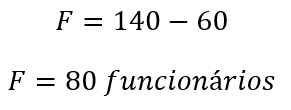
Alternativa E
CESPE – Auxiliar Judiciário/2020
Determinado equipamento é capaz de digitalizar 1.800 páginas em 4 dias, funcionando 5 horas diárias para esse fim. Nessa situação, a quantidade de páginas que esse mesmo equipamento é capaz de digitalizar em 3 dias, operando 4 horas e 30 minutos diários para esse fim, é igual a:
a) 2.666.
b) 2.160.
c) 1.215.
d) 1.500.
e) 1.161.
Na primeira situação (digitalização de 1.800 páginas), a equipe trabalha 20 horas (4 dias x 5 horas diárias); já na segunda situação, a equipe trabalhará 13,5 horas (3 dias x 4,5 horas diárias), assim:

Obs. 30 minutos é metade de uma hora, então podemos dizer que 4 horas e 30 minutos é equivalente a 4,5 horas. A conta é simples, basta dividir os minutos por 60.
Analisando a proporcionalidade: Quanto mais páginas precisam ser digitalizadas, mais horas serão gastas.

Agora é só realizar o cálculo:
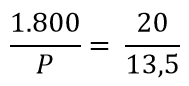
Multiplicando em “X”:
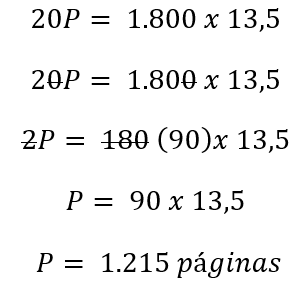
Alternativa C
Vejamos agora a aplicação da regra de três composta com dois exercícios de concurso.
Exemplos de regra de três composta
FCC – Auditor Fiscal de Manaus/2019
Se 3 painéis solares fotovoltaicos produzem 70 kWh de energia em 50 dias, o número de painéis solares que produzem 112 kWh de energia em 15 dias é:
a) 12.
b) 15.
c) 14.
d) 16.
e) 13.
Aplicação bem direta de uma regra de três composta, iniciaremos pela tabela:

Analisando a proporcionalidade: Quanto mais painéis, maior a produção de energia e menor a quantidade de dias necessários para produção, assim:

Então,
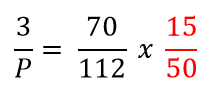
Obs. Note a inversão da fração da variável “Dias”.
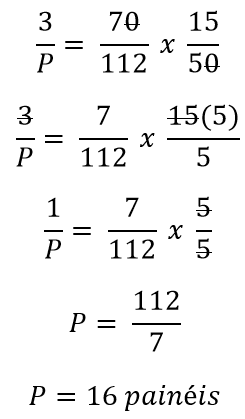
Alternativa D
CESPE – Auditor-Fiscal SEFAZ RS/2019
Em uma fábrica de doces, 10 empregados igualmente eficientes, operando 3 máquinas igualmente produtivas, produzem, em 8 horas por dia, 200 ovos de Páscoa. A demanda da fábrica aumentou para 425 ovos por dia. Em razão dessa demanda, a fábrica adquiriu mais uma máquina, igual às antigas, e contratou mais 5 empregados, tão eficientes quanto os outros 10.
Nessa situação, para atender à nova demanda, os 15 empregados, operando as 4 máquinas, deverão trabalhar durante
a) 8 horas por dia.
b) 8 horas e 30 minutos por dia.
c) 8 horas e 50 minutos por dia.
d) 9 horas e 30 minutos por dia.
e) 9 horas e 50 minutos por dia.
Vamos montar nossa tabela:
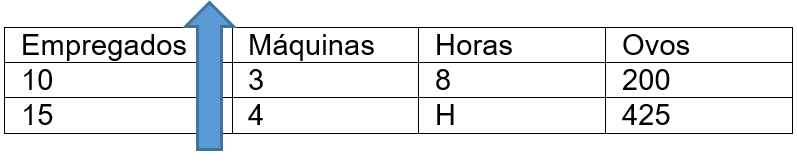
Analisando a proporcionalidade: Quanto mais empregados, menos máquinas serão necessárias, assim como menos horas precisarão ser trabalhadas, além disso, há uma produção de ovos maior, logo:
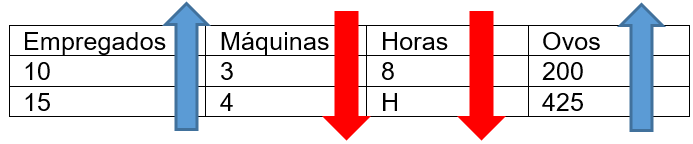
Assim,
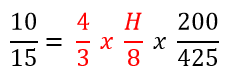
Agora vamos resolver:
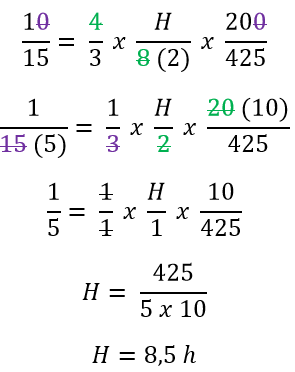
E 8,5h é equivalente a 8 horas e 30 minutos (0,5 x 60 = 30 min)
Alternativa B
Considerações Finais
Caso ainda necessite de mais um reforço, sugiro o curso de matemática básica aqui do Estratégia.
Inclusive, há algumas aulas demonstrativas de regra de três excelentes, não deixe de conferir.

Muitas vezes nosso problema com matemática está na “base”, se for o caso, sugiro essa série de vídeos – Matemática para iniciantes.
É isso aí, pessoal! Espero que o artigo de hoje tenha colaborado com seus estudos de regra de três. Nos vemos na próxima.
Abraço
Assinatura Anual Ilimitada*
Prepare-se com o melhor material e com quem mais aprova em Concursos Públicos em todo o país. Assine agora a nossa Assinatura Anual e tenha acesso ilimitado* a todos os nossos cursos.
ASSINE AGORA – Assinatura Ilimitada
Fique por dentro de todos os concursos: