Teorema de Menelaus: quando que eu posso usar e para que serve?

Olá, jovem estudante, como vai você? Tudo tranquilo? E como andam os seus estudos? Ainda pensando na falácia eterna de que seu rendimento não está bom? Um passo de cada vez, nunca se esqueça disso. Se a cada dia você considerar um passo a frente além do seu dia anterior, ao final do ano você terá mais de 360 passos além do início de seu ano. Vê como faz uma grande diferença? Não se perca, hein? Bom, vamos então falar do Teorema de Menelaus

O Teorema de Menelaus é um teorema relacionado à geometria plana. É um teorema do tipo configuracional. Isso significa que se trata de um teorema que depende da posição relativa entre duas figuras, no caso, um triângulo e uma reta. Mas não se preocupe se não está pegando tudo o que estou falando. Fique calmo que eu vou explicar tudo bem detalhado para você.

Vamos começar considerando um triângulo ABC qualquer e vamos fazendo algumas experiências com ele.

Eis então o nosso triângulo. Se você não está acostumado com geometria plana, relaxe. Quando digo que pode ser um triângulo qualquer, quero dizer que não tem nenhuma particularidade, ok? É apenas isso, nada demais. Continuarei agora realizando construções em cima de nosso triângulo. É sobre ele que daqui a pouco trataremos do Teorema de Menelaus.

Agora, farei uma construção geométrica muito simples; vou desenhar as retas suportes dos lados desse triângulo. Isso será feito para que possamos analisar melhor algumas estruturas internas e externas que aparecerão nesse triângulo daqui a pouco, quando o cortarmos. Esses detalhes iniciais serão importantíssimos para um melhor entendimento de todo o conteúdo acerca do Teorema de Menelaus. Agora, vamos traçar essas retas suportes. Observe:

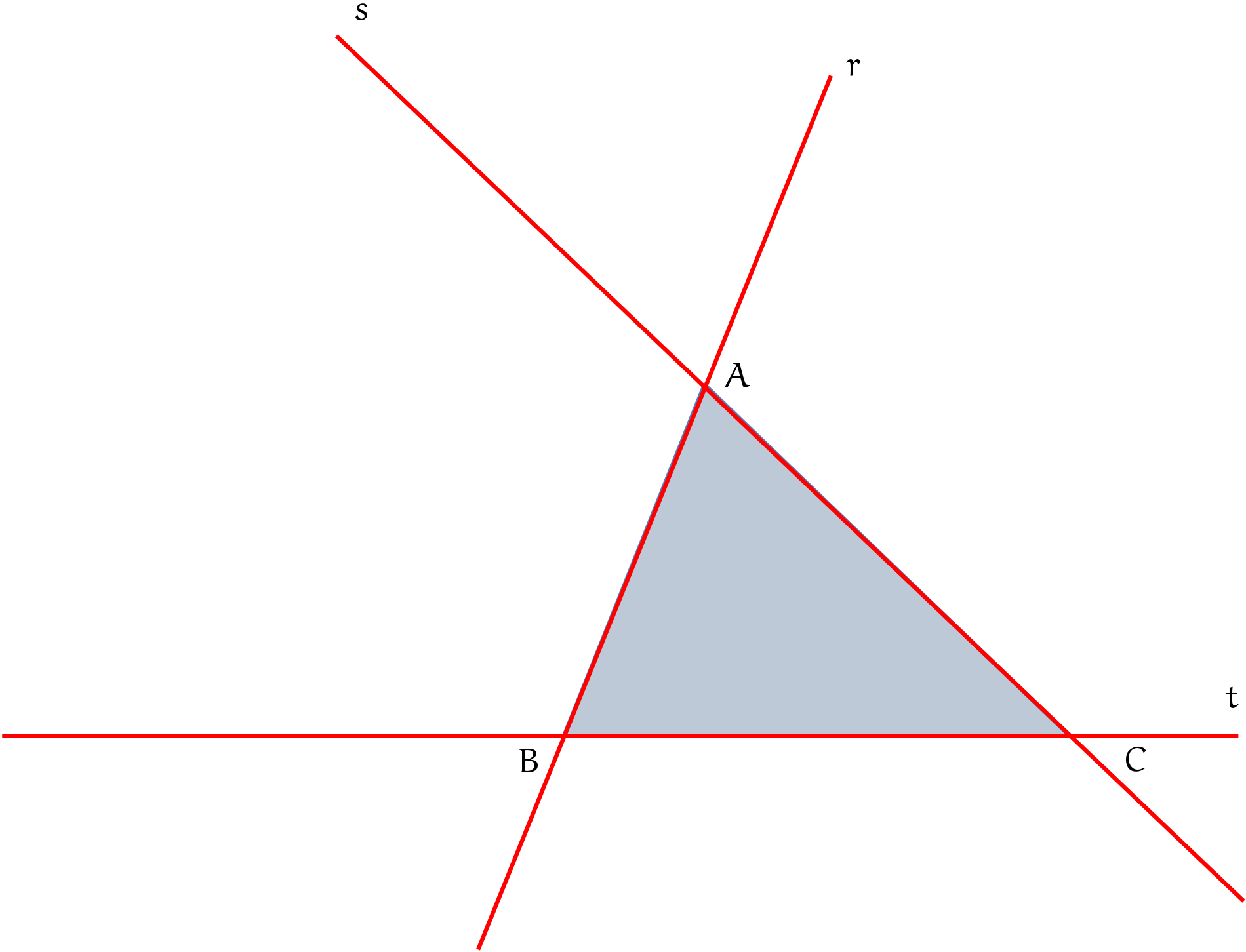
“Professor, mas o que são retas suportes?“

Calma, meu/minha jovem. Vou te explicar. Uma reta suporte de um segmento é a reta que contém aquele segmento. Por exemplo, pegue um caderno agora e marque um ponto nele. Sério, vá lá e o faça. Marcou? Chame esse ponto de A. Agora, marque um outro ponto nesse caderno, distinto de A. Chame esse ponto de B. Fez isso? Agora desenhe, com uso de uma régua, a reta que passa por A e B. Você acabou de “desenhar” a reta suporte do segmento AB (coloco aqui a palavra desenhar entre aspas porque você, na verdade, não traçou reta alguma, visto que retas são infinitas).

O que fiz na minha figura, então, foi simplesmente desenhar as retas suportes dos três lados desse triângulo (que, lembrem-se, também são segmentos de reta): as retas r, s e t.

Agora vamos à particularidade que nos leva à utilização do Teorema de Menelaus. Considere uma reta que corte as três retas suportes desse triângulo (de preferência uma que não contenha um vértice). Vejamos uma situação em que isso aconteça:

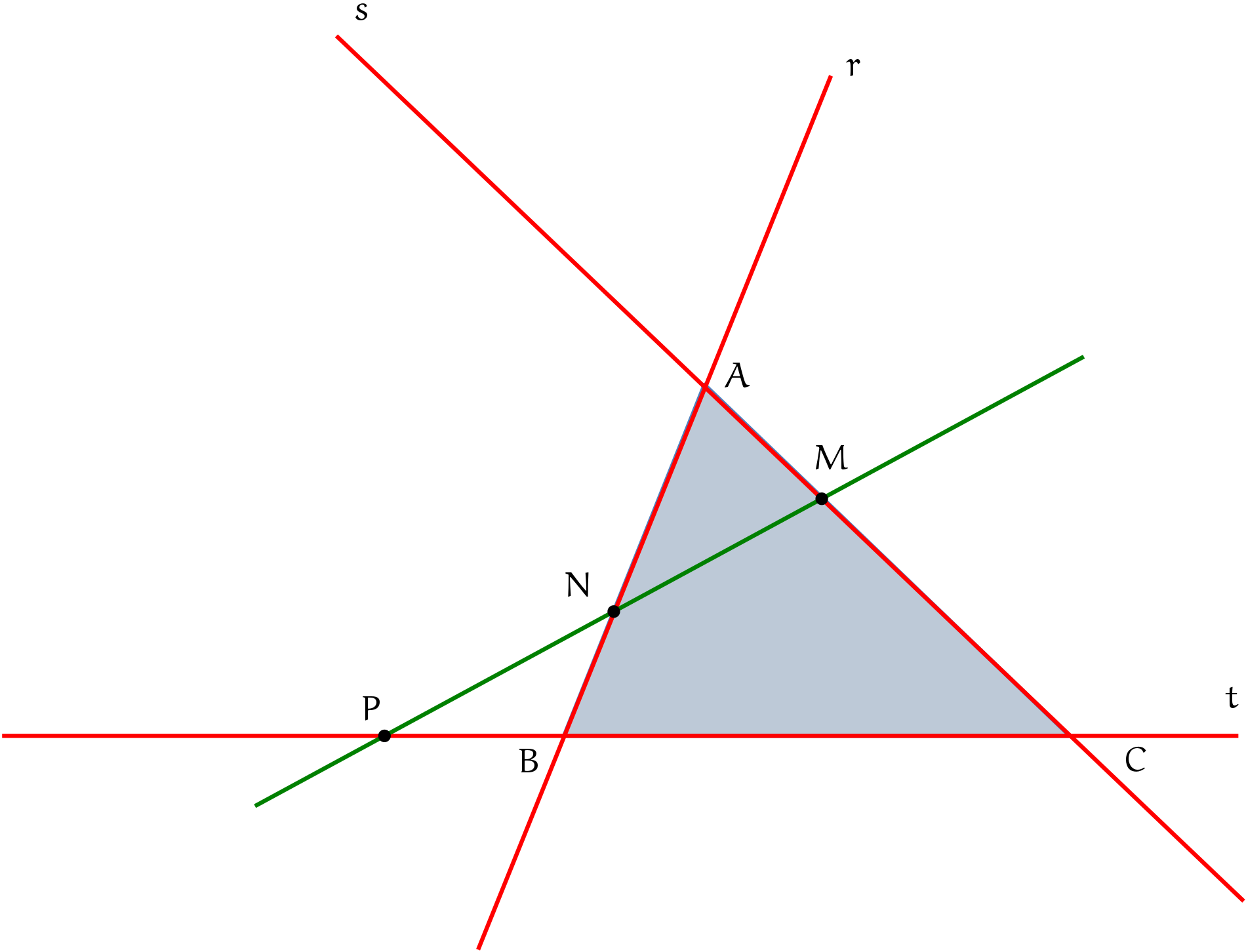
Vê a reta verde? Vê que essa reta corta as retas suportes construídas em vermelho? Essa é uma situação que você olha e deverá, a partir de agora, gritar na sua cabeça: Teorema de Menelaus!

Então, mantenha isso na sua cabeça: a aplicação do Teorema de Menelaus se dá na situação específica em que uma reta corta as retas suportes dos lados de um triângulo em três pontos distintos. Situação como a que vimos acima. Veja uma outra situação possível:

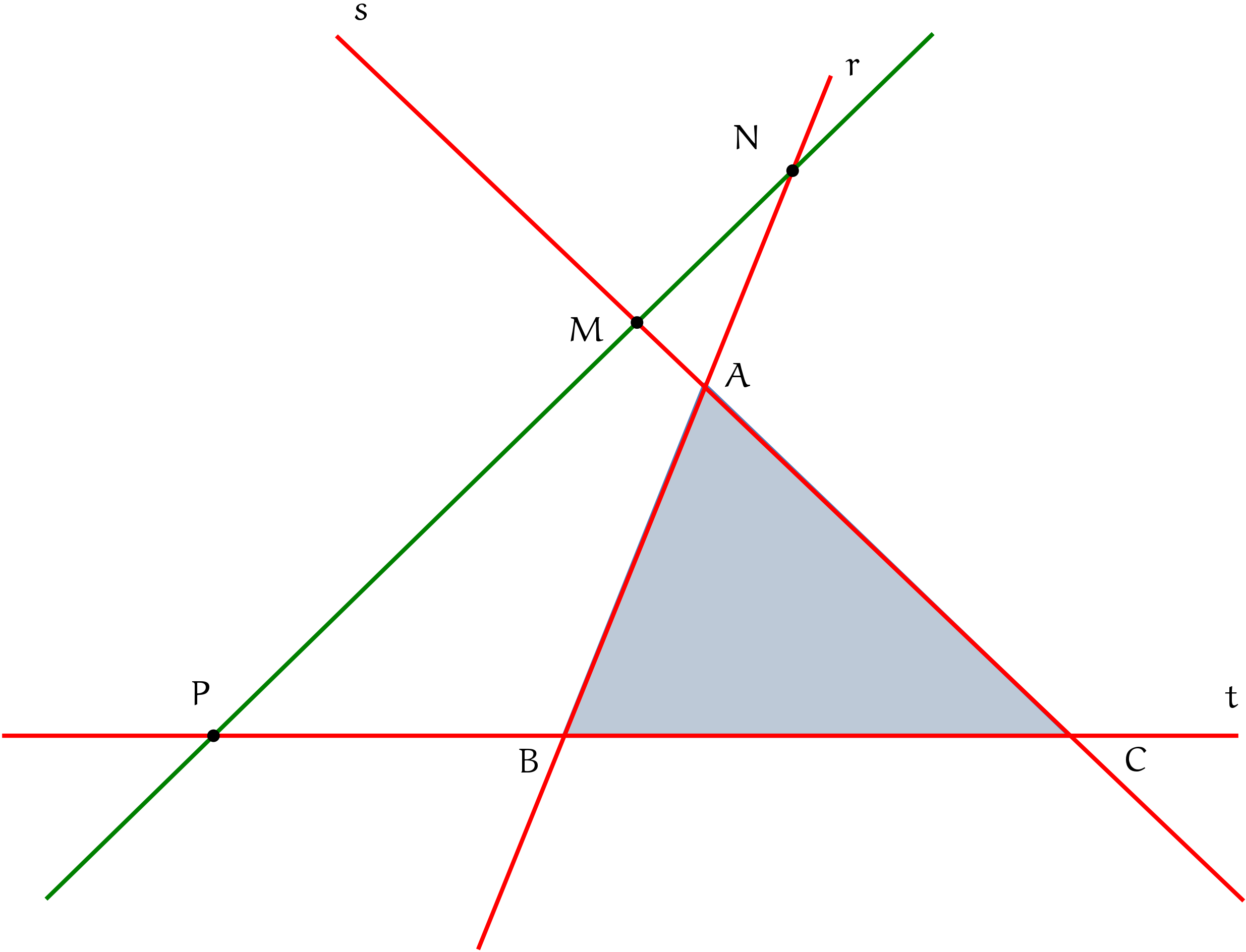
Consegue ver uma grande diferença entre as Figuras I e II ? A principal diferença está nos pontos em que a reta verde corta as retas vermelhas. Veja que na Figura I, a reta verde corta o triângulo em dois pontos internos (M e N) e apenas um externo (ponto P). Já na Figura II, a reta verde corta o triângulo em três pontos externos. Independentemente do caso, o Teorema de Menelaus funciona.

Bom, nossa discussão até agora foi sobre a aplicabilidade do teorema de Menelaus, certo? Agora, vamos procurar entender para que ele serve, qual a sua utilidade (deixando bem claro que eu não o demonstrarei aqui, meu objetivo é te mostrar os quês práticos do teorema em questão).

O Teorema de Menelaus serve para relacionar as razões em que os pontos M, N e P cortam os lados a que pertencem. Vejamos uma forma de memorizá-lo.

Primeiro, desenhe três símbolos de frações, multiplique esse esses símbolos e iguale o produto a 1:

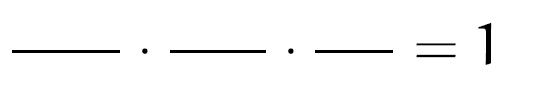
Agora, escreva sobre e sob cada uma das frações, os pontos de corte da reta verde com o triângulo (em nosso caso, M, N e P):

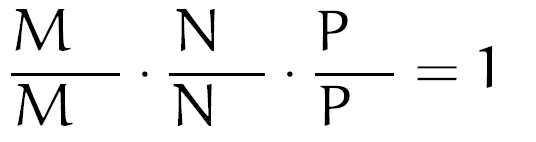
Agora, você deverá se fazer a seguinte pergunta. O ponto M está conectado a quais vértices do triângulo? Dê uma olhada lá nas nossas figuras I e II e tente descobrir.

Olhou? Pois bem, você pode perceber que o ponto M está conectado aos vértices A e C de nosso triângulo, certo? Então, você deve escrever (em qualquer ordem) A e C ao lado do M já escrito na nossa fórmula incompleta. É mais fácil vendo acontecendo, olhe:

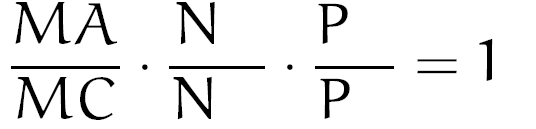
Vê o que fiz? Escrevi A e C ao lados dos M’s já escritos. E sim, poderia ser na ordem que você quisesse. Eu escolhi essa mas sem razões especiais.

Em seguida, devemos pensar da seguinte forma: finja que as letras que estão em cima e embaixo dos sinais de fração podem ser cortar, como se fossem variáveis na álgebra. Lembrem-se de que isso é só uma estratégia para podermos escrever o Teorema de Menelaus. Analise agora os vértices aos quais N está conectado. Analisando as figuras, podemos ver que em qualquer uma das duas situações, N está conectado aos vértices A e B. Só que, agora, não podemos mais dispô-los em qualquer ordem ao lado do N. Devemos colocá-los de modo que se cortem com as letras já presentes. Vou deixar mais claro.

Veja que nossa fórmula até agora possui um A na parte superior, certo? Então o nosso próximo A deverá estar na parte inferior, de forma que nosso próximo preenchimento fica da seguinte forma:

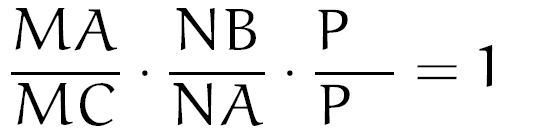
Em hipótese alguma você poderia ter preenchido da forma abaixo:

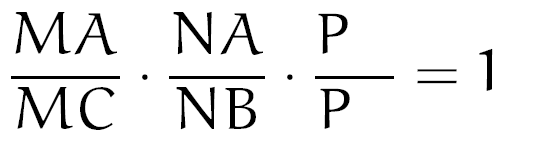
A razão disso é que, da forma que estamos aprendendo a memorizar a fórmula, o truque é que duas letras nunca podem estar em cima ou embaixo simultaneamente, elas devem se alternar. Então se uma das letras A está em cima, a outra deverá estar embaixo. Tudo certo até aqui? Tente você mesmo, agora, a partir do que já leu até aqui, preencher a nossa última fração. Daqui a pouco você enxergará o Teorema de Menelaus de uma forma muito mais mecânica!

Conseguiu? Então, o ponto P está conectado, nas nossas figuras, aos vértices B e C, certo? Então são eles que deverão aparecer na nossa última fração. Mas quem vai para cima e quem vai para baixo? De acordo com o que aprendemos sobre o Teorema de Menelaus, como já existe um B em cima, esse último B deverá aparecer embaixo, certo? Dessa forma:

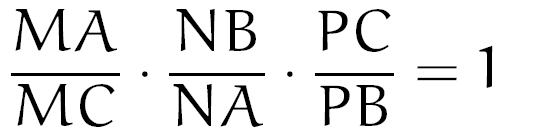
Acima temos, então, o famoso Teorema de Menelaus! Vejamos um exemplo de sua aplicação, assim assentamos a nossa teoria!!!

Questão [Escola Naval]

O triângulo da figura abaixo é equilátero, AM = MB = 5 e CD = 6.

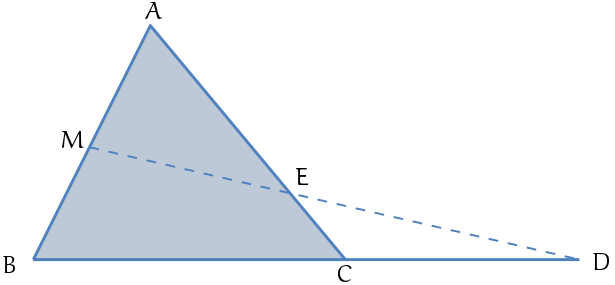
A área do triângulo MAE vale:

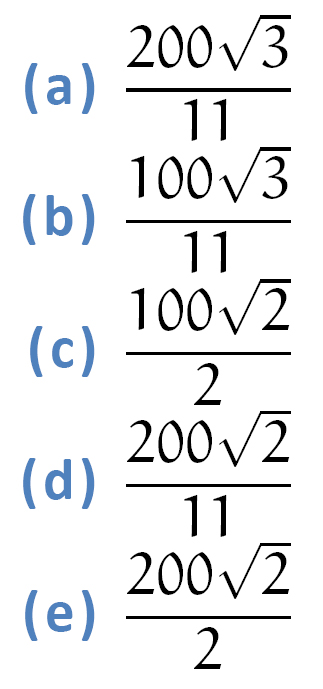
SOLUÇÃO

Vamos então à nossa solução. Existe uma forma de calcularmos a área de um triângulo que envolve a metade do produto de dois lados pelo seno do ângulo adjacente (os nossos pacotes de geometria cobrem toda essa teoria com muitos exemplos). Em nosso caso, Sabemos a medida AM, sabemos a medida do ângulo BAC (60º), porém, não sabemos a medida de EA. Agiremos, então, tentando encontrar essa medida. Em primeiro lugar, observe a situação que caracteriza o Teorema de Menelaus: um triângulo ABC, cortado por uma reta nos pontos: D, E e M.

Vejamos como ele pode nos ajudar a resolver esse problema. Começamos o Teorema de Menelaus montando as nossas frações, como te ensinei:

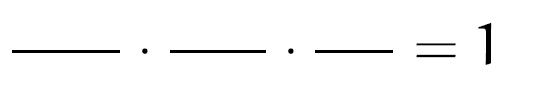
Agora, podemos adicionar os pontos em que a reta corta o nosso triângulo:

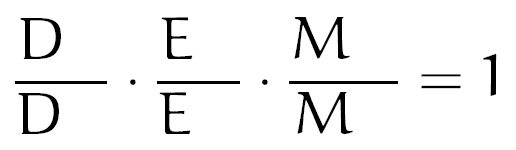
O ponto D está conectado aos vértices B e C. Podemos, então, colocá-los na ordem que quisermos:

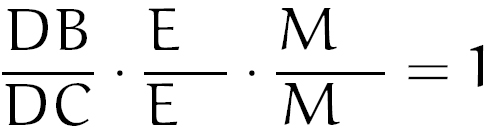
Agora, veja que o ponto E está conectado aos vértices A e C. Mas agora, não podemos mais colocá-los em qualquer ordem. Pelo que estudamos do Teorema de Menelaus, vimos que o ponto C deverá estar acima, pois o C anterior está embaixo. Ficamos, então, com o seguinte preenchimento:

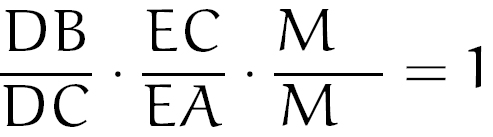
Finalmente, veja que o ponto M está conectado aos vértices A e B. Como o A anterior está embaixo, esse só poderá estar acima, nesse formato:

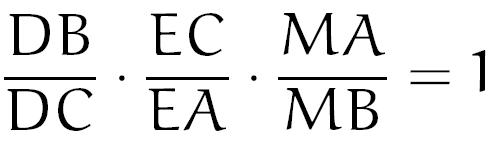
E pronto. Temos a nossa expressão pronta. Agora, deveremos usar nosso conhecimento geométrico para continuarmos a questão. Sabemos que o triângulo é equilátero. Dessa forma, temos que o seu lado mede 10, visto que AM = MB = 5. Dessa forma, BC = 10. Como CD = 6 (informado pelo problema), então temos que DB = 10 + 6 = 16. Podemos então, substituir esses valores na expressão encontrada:

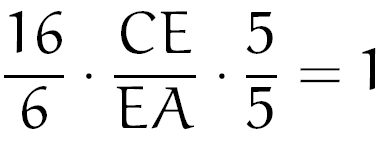
Prosseguindo com a nossa conta, encontramos:

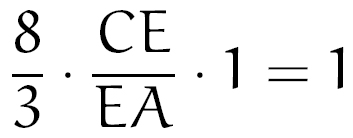
Isolando CE, temos:

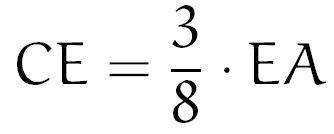
Mas sabemos que:

Então, temos que:

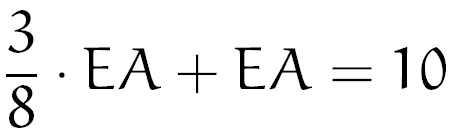
Resolvendo essa equação, oberemos:

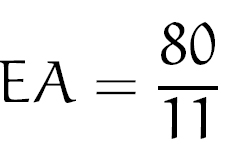
Daí, podemos calcular a área do triângulo pedido:

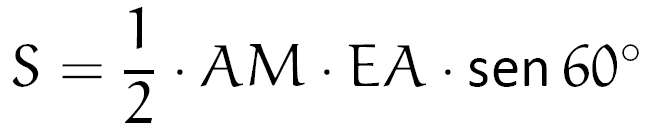
Fazendo as substituições:

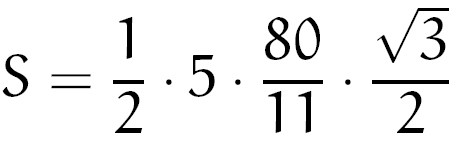
Fazendo as contas, conseguimos concluir que a área S procurada é:

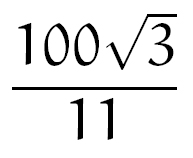
E é isso meu/minha jovem, espero que tenha sido de boa utilidade para você!! Não se esqueça de checar os nossos cursos, com resolução de todas as questões do seu concurso paralela a uma teoria detalhada e mastigada em vídeo e em PDF. Seguem os nossos principais pacotes de preparação em geometria (é só clicar em cima do desejado):

EEAr, EsSA, EAM, CFN, CN, EsPCEx, EFOMM

Deixo aqui também um link para a Wikipédia acerca do teorema de Menelaus.

Se quiser saber um pouco mais sobre triângulos, tenho um artigo comentando sobre o baricentro de um triângulo. Se quiser dar uma olhada nele, é só clicar aqui.

Um grande abraço para você!!!